[Theme 07] Back Propagation 설명

안녕하세요 pulluper 입니다. 😄

 

이번 포스팅은 드디어 Back Propagation에 대하여 다뤄보도록 하겠습니다. 

지난 시간에 다룬 MLP에 대하여 이어서 다뤄보겠습니다.

다음과 같은 MLP 가 있다고 하겠습니다. 

그림 1. MLP

이를 그림으로 표시하면 다음과 같습니다.

2개의 feature 를 갖는 하나의 input을 네트워크에 넣었을때의 그림입니다.

 

그림 2. MLP 네트워크구조

x1, x2 에서 h1, h2, h3 로 갈때를 수식으로 표현하면 다음과 같습니다. 

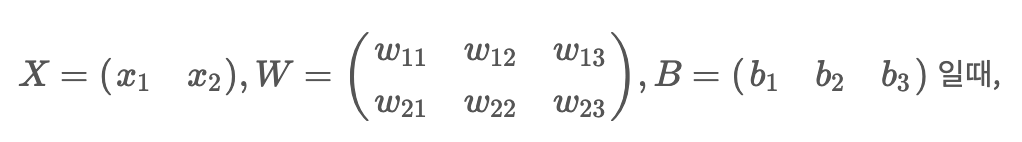
(h1, h2, h3) = $\phi$ (XW + B) 로 표현할 수 있습니다. $\phi$ 는 activation function 입니다.

혹은 다음과 같이 XW + B 를 matrix multiplication으로 한번에 표현 할 수 있습니다. 

이런 방식으로 전체 네트워크 output을 $f_{\{w, b\}}(x)$ 로 표현 할 수 있습니다. 

여기서 각 w, b들을 학습 시키기 위해 필요한 방법이 오늘 알아볼 back propagation 입니다. 

이를 위해 간단한 구체적인 예시부터 일반화하는 식으로 알아보겠습니다. 

---

이를 위해 참고해야 할 부분을 먼저 보겠습니다. 

 

1.  Chain Rule (합성함수의 미분법)

Chain Rule

함수 $f : X \rightarrow Y , g : Y \rightarrow Z$가 모두 미분가능하고 

함성함수 $F(x) = g(f(x)) = g \circ f (x) $, $(x \in X)$의 미분은 다음과 같다. 

$F'(x) = g'(f(x)) f'(x)$ 즉, 두 함수의 미분의 곱과 같다.

$z = g(y), y = f(x)$일때, 

$\Leftrightarrow \frac{\partial z}{\partial x} = \frac{\partial z}{\partial y} \frac{\partial y}{\partial x}$ 와 같다.

 

2. Loss function (손실함수)

Loss(Cost) fucntion 이란 네트워크를 학습시키기 위한 기준으로 

ouput과 정답간의 차이를 측정할 수 있는 함수입니다. 

이는 다음과 같이 쓸 수 있습니다. 

$L : X \times Y \rightarrow Y$ 

$L(f_{\theta} (X), Y)$ or $L(X, Y | \theta)$

 

3. Gradient Descent (경사하강법)

GD(gradient descent)

경사하강법은 최적화 방법의 하나로 다음을 구하기 위한 구체적인 방법입니다.

$argmin_{\theta} L(X, Y|\theta)$

$\theta = \theta - \eta \nabla_{\theta} L(X, Y| \theta)$, iteratively

우리의 목표는 손실함수를 최소화하는 parameter들을 찾는 것 입니다.

여기서의 parameter 는 (weight, bias)를 모두 포함합니다. 

이를 위해서 각 Loss 에 대한 parameter의 변화율을 구하여 update 를 해 주어야 합니다.

여기서 결정해야 하는것은 얼마나 반복할 것인지, 초기값은 무엇일지, learning rate를 무엇으로 정할지 입니다. 

---

Back Propagation 

 

로스에 대한 모든 파라미터의 변화율을 구하는 방법을 back propagation 이라고 합니다. 

이를 그냥 구할수도 있지만, 출력노드의 미분값을 그 전노드들에게 전달하면서 재사용하는 방법입니다. 

가장 마지막 layer, activation function의 미분과 chain rule 을 이용하여 이어진 그래프의 전체 

parameter(weight, bias)에 대한 미분을 계산 할 수 있는 일종의 다이나믹 프로그래밍 알고리즘이라 할 수 있습니다. 

 

어떤 deep neural network는 여러 함수들의 합성으로 볼 수 있습니다.

가령 위에서 정의한 1개의 hidden state를 갖는 mlp는 $\phi^2 (\phi^1(XW^1 + B)W^2 + B)$ 로 볼 수 있습니다. 

우리는 chain rule로써 합성함수들에 대한 미분값을 알 수 있습니다. 

 

이제 실제 예를 들어 알아보겠습니다. 

다음과 같은 hidden layer 가 1개인 뉴럴 네트워크를 생각해 보겠습니다. 

그림 3. 역전파를 위한 모델

 

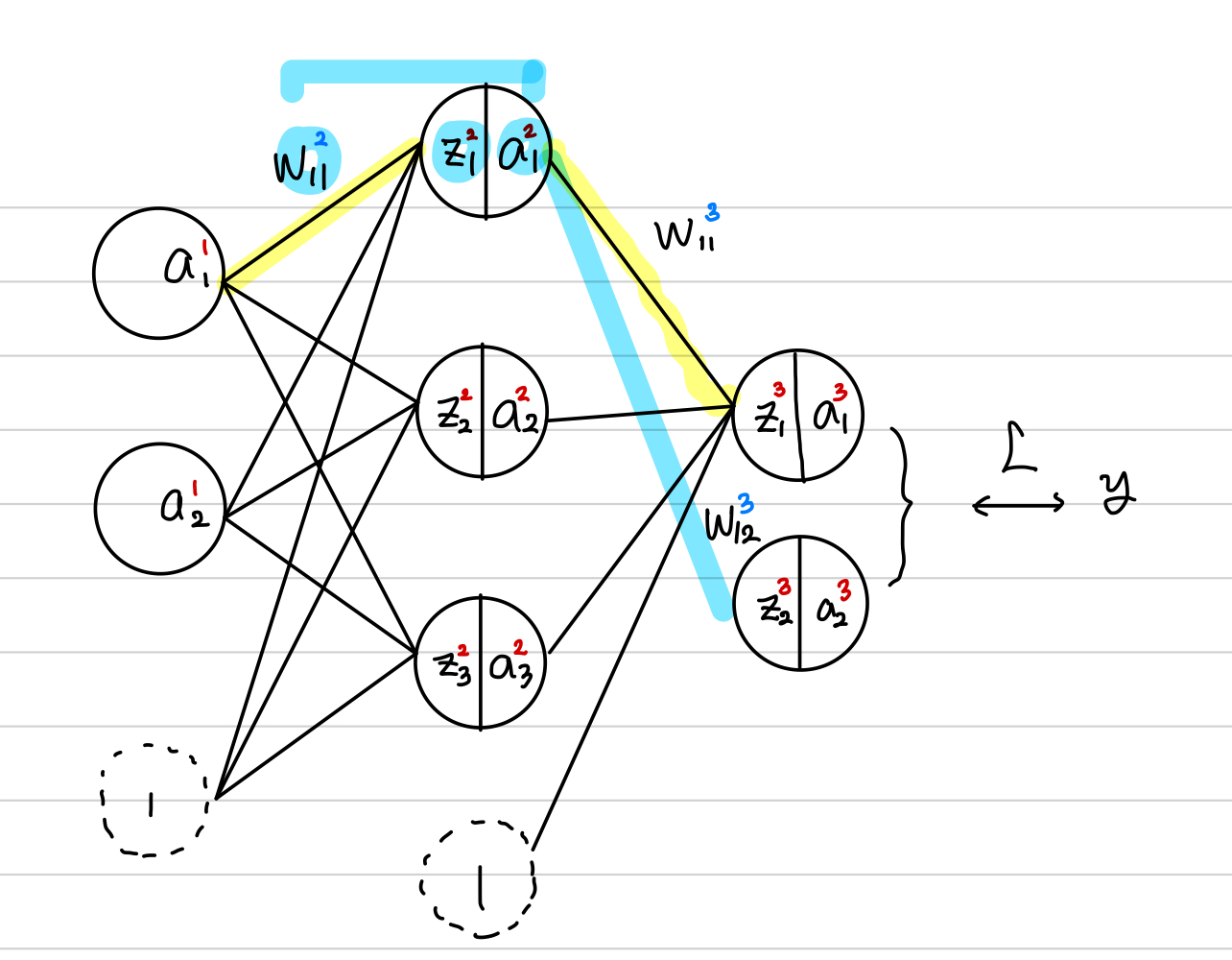
목적은 모든 parameter(w, b) 에 대한 L의 변화율을 구하는 것 입니다. 

그림 4. 역전파의 목적

 

먼저 순전파의 pass 를 보면, 각 $z^l, a^l$ 에 대한 수식은 다음과 같습니다.

 

그림 5. 순전파(forward pass)

 

그리고 Loss 는 다음과 같이 MSE 로 정했습니다.

그림 6. Loss 함수

 

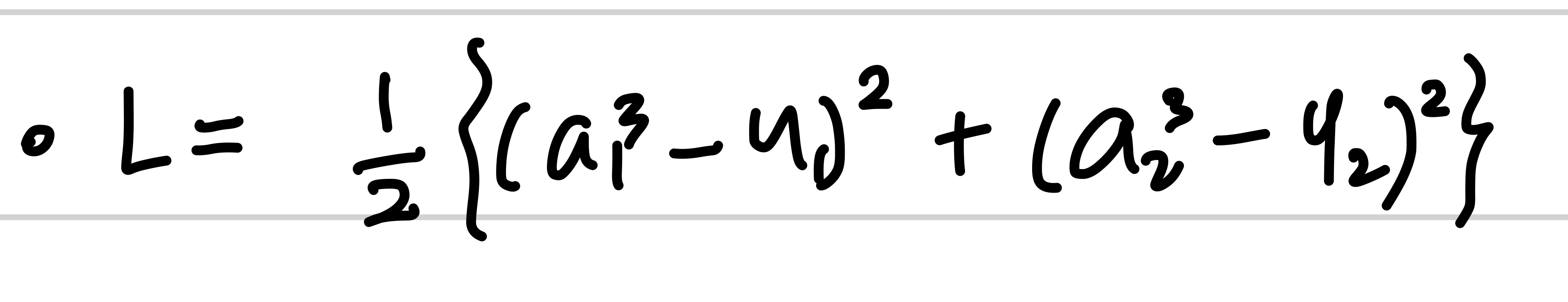
이제 역전파로 w에 대한 L의 미분들을 구해보겠습니다.

먼저 위의 그림에서 $W_{11}^3$ 에 대한 L의 미분은 $\frac{\partial{L}}{\partial{W_{11}^3}}$ 

다음과 같이 전개됩니다. 

 

그림 7. 역전파1

 

각각은 그림 5의 순전파의 수식에 의해 다음과 같이 미분됩니다. 

이번에는 더 앞의 w 인 $W_{11}^2$ 에 대한 L의 미분을 보면, 다음과 같습니다. 

 

그림 8. 역전파 2

 

$\frac{\partial{L}}{\partial{W_{11}^2}}$ 는 다변수 함수의 편미분에 대한 chain rule 을 이용합니다. 

여기서 일반화를 위해 $\delta_a^l$ 라는 변수를 activation의 미분값과 마지막 노드와의 미분의 곱으로 정합니다. 

 

그림 9. 역전파 3

 

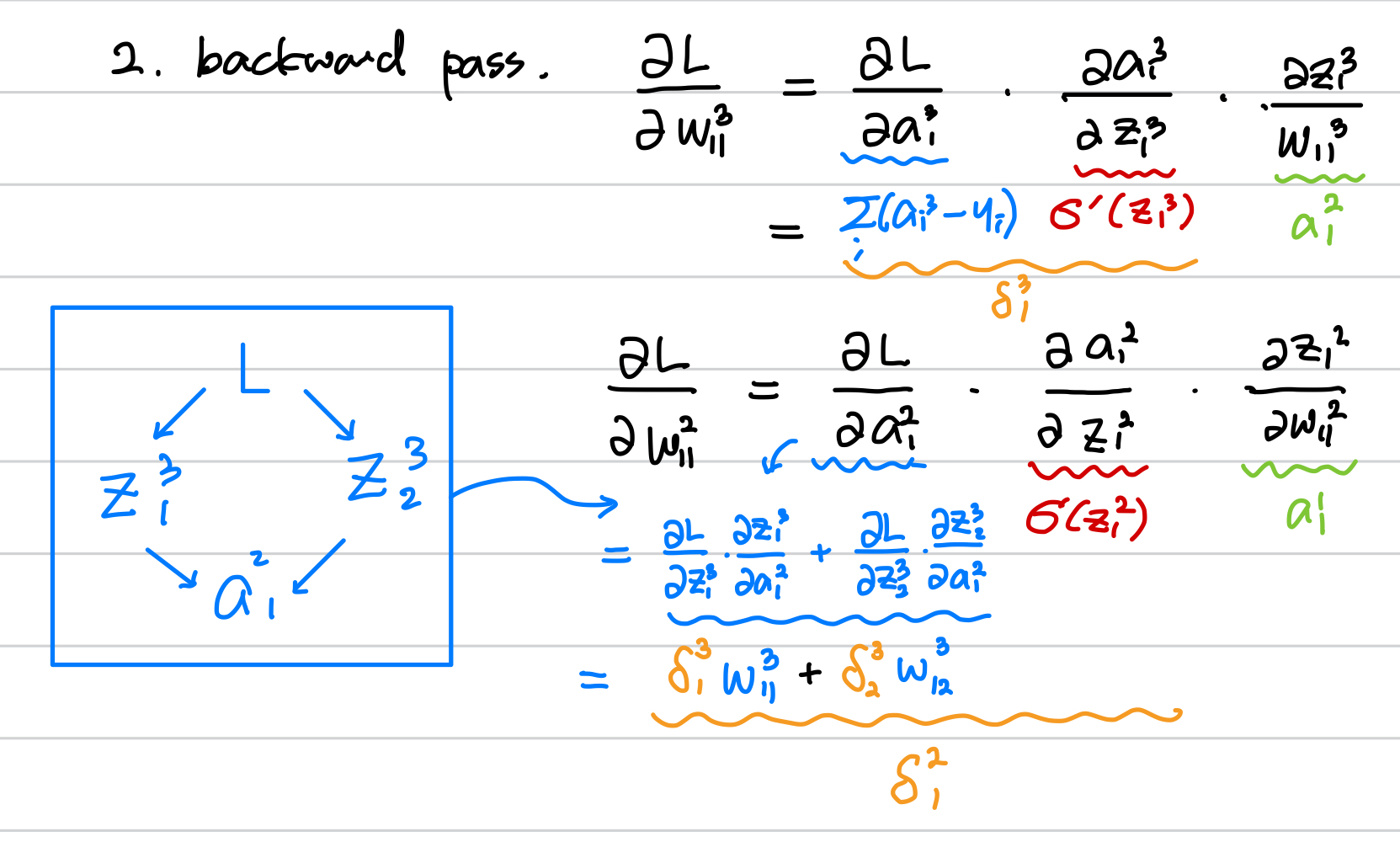
이를 정리하면 델타는 다음과 같이 재귀함수로 일반화가 되고,

이를 이용하면, 임의의 w, b에 대하여 미분값을 구할 수 있게 됩니다. 🥲🥲🥲

 

그림 10. 역전파 4

 

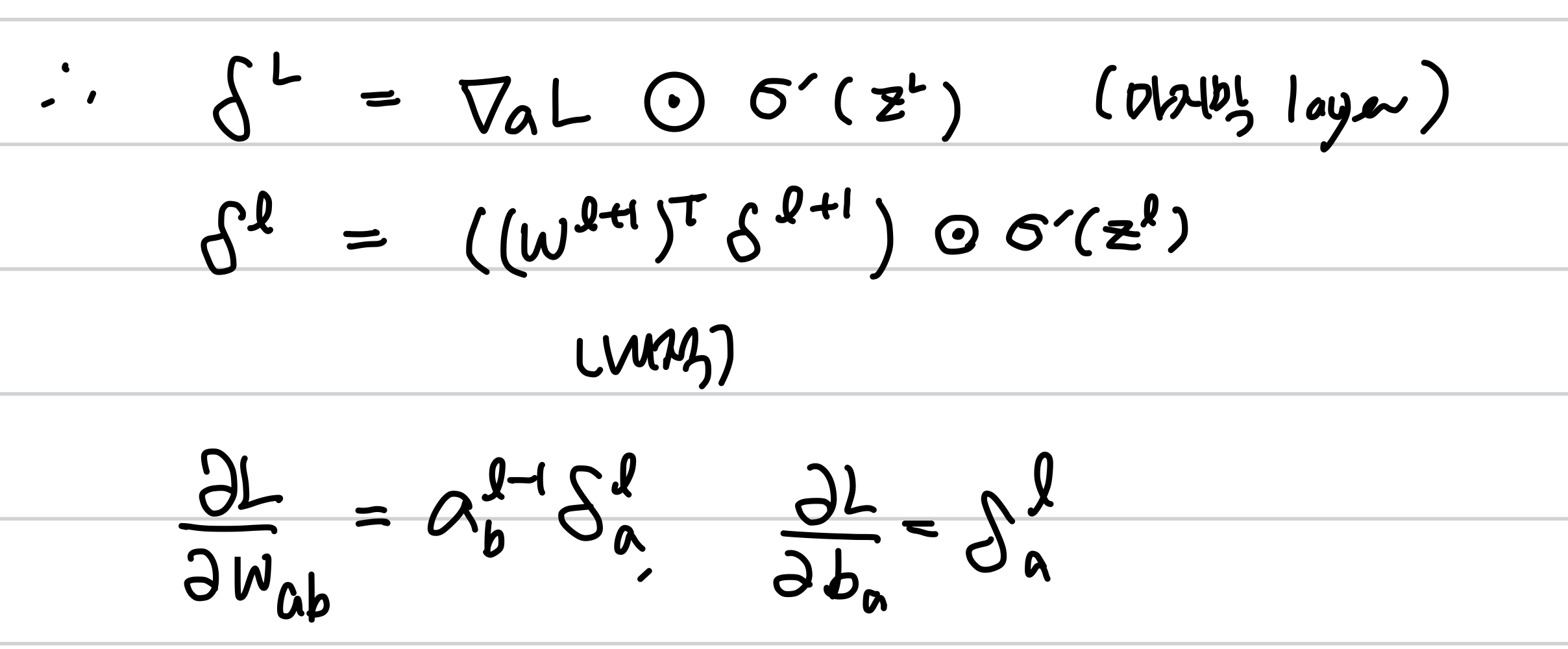
이전의 delta 값과 activation 의 도함수, 그리고 forward pass의 a 값들로 앞으로 전달되면서

각 parameter 에 대한 미분값을 업데이트 할 수 있기 때문에 뒤로 전파된다는 back propagation이라 합니다. 

---

이번 포스팅에서는 딥러닝을 update 하는 Gradient Descnet 방법과

임의의 w, b에 대한 미분값을 구하는 backprogation에 대하여 알아보았습니다. 

질문과 댓글은 큰 힘이 됩니다. 

감사합니다. 😎😎😎😎