[Theme 04] Multinomial Logistic Regression (Softmax Regression)

안녕하세요 pulluper 입니다. 🔗 이번 포스팅에서는 다중 클래스 분류를 위한 multinomial logistic regression (softmax regression) 에 대하여 알아보겠습니다. 목적은 여러 클래스의 분류를 위함입니다. 예로는 MNIST, CIFAR, Imagenet 등 여러 데이터에서 각 사진에 대한 class label 을 판단하는 문제를 들 수 있습니다.  

examples of mnist / cifar / imagenet

---

먼저 예를 들어서 sigmoid 와 softmax 방법의 차이를 알아보겠습니다. 이번에도 철수에 관한 이야기입니다. 철수는 저번의 실수 이후로 데이터 분석에 관심이 생겼습니다. 철수는 공부시간과 수업참석에 따른 학점을 분류하고 싶었습니다. 그래서 다음과 같은 data를 얻었습니다. 

시간, 참석, 성적에 관한 data

이를 그래프로 나타내면 아래 그림의 왼쪽과 같습니다. 어떻게 하면, 각 성적대로 분류를 할 수 있을까요? 아래 그림의 오른쪽처럼 철수는 배웠던 logistic regression을 기준으로 각 클래스와 그 클래스가 아닌 것들을 구분하는 방법으로 3번의 logistic regression을 사용하도록 설계를 했습니다. 

 

여기서 $X$에 $W_A, W_B, W_C$를 곱해서 학습해야 하고, sigmoid 함수를 통해 logistic regression 을  3번 계산합니다. 

이것의 실제 연산은 다음과 같습니다.

각 데이터의 output 은 class 별로 0 ~ 1 사이의 값을 가지고 있습니다. 즉, 각각의 output들이 독립적으로 특정(target) 클래스일 확률을 출력합니다. 따라서 하나의 data의 확률 output들의 합은 1이 아닙니다. 예를들어 위의 결과에서 첫번째 row 는 [0.77, 0.3, 0.8] 로 나올 수 있습니다. 즉 sigmoid 는 각 출력 값을 클래스마다 개별적으로 봅니다. 

softmax 의 예

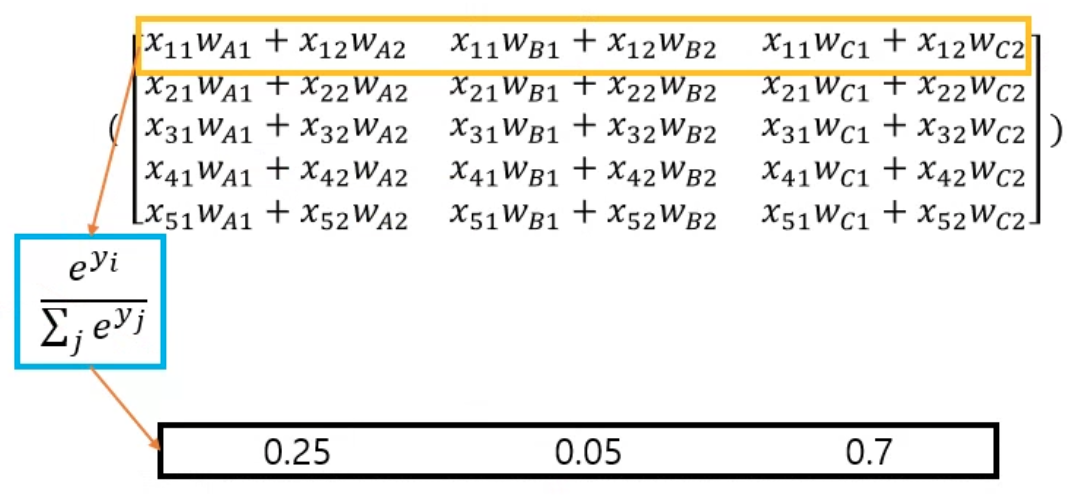
반면에 softmax의 출력은 모두 상호 연관되어 있습니다. 예를들어 이번에는 softmax 를 사용해서 [0.25, 0.05, 0.70] 의 확률이 나왔습니다. (softmax 의 수식은 위의 그림과 같습니다) softmax에 의해 생성된 확률은 설계상 항상 0.25 + 0.05 + 0.70 = 1.00으로 합산됩니다. 따라서 softmax를 사용하는 경우 한 클래스의 확률이 증가하려면 다른 클래스 중 하나 이상의 확률이 동일한 양만큼 감소해야 합니다. 

 

그렇다면 어떤 방법을 어디에 사용하면 좋을까요?

sigmoid 를 사용하는 것은 이는 정답 label이 여러개인(multi-label classification task) 에서는 더 알맞습니다. 

softmax 는 하나의 데이터의 class 가 하나인 분류문제(multi-class classification task) 에서는 더 좋습니다. 

---

이번에는 Softmax 함수의 유도과정을 알아보겠습니다.  

먼저 다음과 같은 bayes' rule 를 보겠습니다. 

 

$P(Y|X)=\dfrac{P(X|Y)P(Y)}{P(X)}$

 

X는 data, Y는 class 이고, P(Y|X) 는 posterior, P(X|Y) 는 likelihood, P(Y)는 prior, P(X)는 evidence 입니다.  

$P(Y_1|X)$의 의미는 무엇일까요? data $X$ 가 $Y_1$ class 일 확률입니다. 이는 다음과 같이 확장될 수 있습니다.

 

$P(Y_1|X)=\dfrac{P(X|Y_1)P(Y_1)}{P(X)}=\dfrac{P(X|Y_1)P(Y_1)}{P(X|Y_1)P(Y_1) + P(X|Y_2)P(Y_2) + ... + P(X|Y_n)P(Y_n)}$

 

여기서 다음과 같은 확률의 전확률의 법칙(law of total probability)과 곱의법칙(multiplicative rule)을 이용합니다.

 

1. 전확률의 법칙(law of total probability) 2. 곱의법칙 (multiplicative rule)

Let $a_k = ln(P(X|Y_k)P(Y_k))$, 이면 위의 식은 $\dfrac{e^{a_k}}{e^{a_1}+e^{a_2}+...+e^{a_k}}$ 로 확장됩니다.

 

즉 정리하면, $P(Y_i|X)$ 를 $\dfrac{e^{a_i}}{\sum_j^k e^{a_j}}$ 로 나타낼수 있고, 이는 softmax 함수입니다. 😎

---

Softmax 함수를 썼을때의 Cross Entropy Loss 를 MLE 를 통해서 유도 해 보겠습니다. 

 

MLE 를 사용하기 위해서는, 적절한 확률분포를 사용해야 합니다. 여기서는 multinomial distribution (다항분포) 를 이용합니다. 위키백과에서 가져온 다항분포는 다음과 같습니다. 

우리는 n번의 시행이 아니라 1번의 시행에서의 i번째 값이 1회 나타날 확룰 (label) 을 구해야 하므로 이를 다음과 같이 쓸 수 있습니다. 

 

                                                                                      $ \prod_i^k P_i^{y_i}$

 

즉, 이 것의 뜻은 k 번째 클래스가 나올 확률은 각 클래스들의 다음곱과 같다는 것 입니다. 우리는 parameter $P_i$ 를 얻기 위해서 이 식에 Log likelihood 를 구할것 입니다. 이는 [https://csm-kr.tistory.com/35] 에서도 말했듯이, 그 확률분포의 pdf 를 사용하면 됩니다. 따라서 위의식은 $\sum_i^k y_i log(P_i)$ 이 되며, MLE에서는 maximum likelihood estimation 이므로, -를 곱한값을 최소화 하는 방향으로 학습을 하게 됩니다. 따라서 우리가 원하는 것은 $ argmin_{\theta} ( - \sum_i^k y_i log(P_i) ) $, Where $P_i = softmax(f_{\theta}(x))$  입니다. 이 수식이 바로 cross entropy 입니다. 

---

이번 포스팅에서는 multi-class 를 위한 softmax 와 cross entropy 를 알아보았습니다. 이번에도 복습을 위한 Quiz 가 준비되어 있습니다. 

 

1. softmax 와 sigmoid 를 사용해서 multi-class,  multi-label task를 풀 때 다른점은?

2. softmax 함수를 베이지안 룰로 유도하세요

3. cross entropy 를 다항분포의 MLE 를 통해서 유도하세요

 

감사합니다. 질문과 토론은 항상 환영합니다. 다음에는 MLE 에 대하여 알아보겠습니다. 감사합니다 ~ 뿅 👏👏👏👏👏

 

Reference

https://hyunlee103.tistory.com/12

https://glassboxmedicine.com/2019/05/26/classification-sigmoid-vs-softmax/

https://ko.wikipedia.org/wiki/%EB%8B%A4%ED%95%AD_%EB%B6%84%ED%8F%AC

https://velog.io/@dayday/%EB%B6%80%EC%8A%A4%ED%8A%B8%EC%BA%A0%ED%94%84-week2-%EC%8B%AC%ED%99%94-%EC%A3%BC%EC%A0%9C