[Theme 02] Linear Regression(선형회귀) (Feat. OLS/GD/MLE)

안녕하세요 Pulluper입니다. 😀

Basic ML 2번째 주제는 supervised learning 의 기본인 Classification / Regression 중 Regression 의 한 종류인 Linear Regression(선형회귀)입니다. 

---

먼저 회귀(Regress) 란 옛날 상태로 돌아가는 것을 의미합니다. 옛날 영국의 유전학자가 부모의 키와 아이들의 키가 선형적인 관계가 있고 전체 키 평균으로 돌아가는 경향이 잇다는 가설을 세웠으며 이를 분석하는 방법을 회귀분석이라고 하였습니다. 이를 알아보기 위해 몇가지 용어들에 대하여 알아보겠습니다. 

통계적 기법에서 회귀란 다음과 같습니다. 

회귀(Regression) : 둘 이상의 변수들 간의 관계를 보여주는 통계적 방법

 

또한 수학적, 통계적 모델에서 사용되는 독립변수, 종속변수는 다음과 같습니다. 

독립변수 (Independent variable) : 다른 변수에 영향을 주는 변수 (원인) [원인,설명,예측]변수

종속변수 (Dependent variable) : 다른 변수로부터 영향을 받는 변수 (결과) [반응,피설명,피예측]변수

 

독립변수는 어떤 결과를 위해서 의도적으로 변화시키는 변수이고 종속변수는 그 결과가 뜻하는 변수입니다. 

---

오늘 다룰 Linear Regression (선형회귀)가 통계적 기법으로 다음 용어들이 필요하기 때문입니다. 위키백과에서 선형회귀를 검색하면 다음과 같이 나옵니다. 

통계학에서, 선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀(simple linear regression), 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다. 

 

즉 X, Y의 간의 관계가 Y = WX + b 선형적인 모델을 따른다는 가정을 가지고 회귀를 하는 것이 선형 회귀입니다.  

예를 들어서 시작해 보겠습니다. 😎😎

---

철수는 이번 중간고사에서 평균 70점 넘으면 엄마가 게임기를 사준다고 하였습니다. 😀

하지만 철수는 공부가 너무 하기 싫었답니다. 그래서 최소한의 노력을 가지고 70점을 넘게 하기 위해서 친구들의 공부시간과 중간고사 성적을 조사하였습니다. 4명을 조사했는데 그 정보는 다음과 같습니다. 

 

x(hours)	y(score)
10	90
9	80
3	50
2	20

 

그리고 하나의 가설을 세웠습니다. "공부시간과 성적은 어떤 직선의 관계가 있겠다." 라는 가설입니다. 

그 직선을 H(x) 라고 하였고, 다음의 관계를 설정하였습니다. H(x) = Wx + b, where x 는 공부시간, H(x) 는 성적입니다. 그렇다면 H(x)를 잘 구해야 철수는 최소한의 노력으로 70점 이상을 맞을 수 있습니다. 

 

 

H(x) 를 구하는 방식으로 각 점과 가설함수 H(x) 에 대한 오차를 설정하고 그 오차를 최소화하는 방향으로 H(x)를 구할 수 있습니다. 오차를 H(x) 와 y의 차이의 제곱들의 평균이라고 설정하면, $\frac{1}{m}\sum_{i=1}^m{(H(x^i)-y^i)^2}$ 이 오차가 됩니다. 

 

cost function

 

아래 그림에서 분홍색이 뜻하는 error들의 제곱의 평균을 뜻합니다. 제곱을 하는 이유는 음수를 나오지 않게 하면서, 큰오차는 더 큰 차이를 내도록 하여 잘 줄이게 하기 위함입니다. 이는 cost function 또는 loss function 등으로 불립니다. 

 

이 오차를 최소화하는 가설 (H(x)) 을 구하고, 70점이 넘도록 공부시간을 최적화 하는 것이 철수의 계획이었습니다. 

그렇다면 어떻게 오차를 최소화 할 수 있을까요?

 

OLS (ordinary least square - 최소제곱법)
GD (gradient descent - 경사하강법)

MLE (maximum likelihood estimation - 최대가능도(우도)법)

 

이 3가지 방법으로 오차를 최소화는 H(x)를 구해보겠습니다 🤪

---

OLS (Ordinary Least Square)

 

 

OLS (ordinary least square) 은 최소제곱법으로 잘 알려져 있으며, 선형 회귀의 가장 기본적인 해결법이 됩니다. 사실 미분을 통해서 error 가 최소가 되는 각 parameter들을 구하는 방법입니다. 통계, 계량경제학에서 나오는 기본적인 내용입니다. 행렬로 표현을 해서 다중회귀분석 (parameter 가 여러개인 선형회귀) 를 푸는데 편합니다. 

 

먼저, H(x) 를 행렬로 표현해 봅시다. $H(x) = Wx + b$에서 $b$ 를 $w_0$ 로, $W$ 를 $w_1$ 으로 바꾸면, $H(x) = w_0 + w_1 x$입 니다. 이는 다음 행렬로 표현 가능합니다. $\begin{pmatrix} 1 & x \end{pmatrix}$ $\begin{pmatrix} w_0 \\ w_1 \end{pmatrix} = w_0 + w_1 x$   $X = \begin{pmatrix} 1 & x \end{pmatrix}, w = \begin{pmatrix} w_0 \\ w_1 \end{pmatrix}$ 일 때, $H(x)$는 $Xw$입니다. OLS에서는 잔차 제곱합 RSS(residual sum of squares) 를 최소화 합니다. 위에서 구한 cost function에서 평균 말고 합을 해 주면 됩니다.

RSS를 구하는 방법은 $(y - Xw)^T (y - Xw)$ 입니다. 위에서 보면 data가 4개가 있는데, 이를 $(x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4)$ 라고 하겠습니다. RSS에서 사용된 $y$ 는 data가 4개 이므로 풀어쓰면 $y = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \\ \end{pmatrix}$ 입니다. 이는 $4 \times 1$ 행렬입니다. $Xw = \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ 1 & x_3 \\ 1 & x_4 \end{pmatrix} \begin{pmatrix} w_0 \\ w_1 \end{pmatrix}$ 로 계산하면 $4 \times 1$ 의 행렬(벡터)입니다! 

 

따라서 $(y - Xw)^T (y - Xw)$ 는 하나의 스칼라 값을 갖게 되고, 이는 여러 data들의 잔차의 제곱의 합을 뜻합니다. 우리는 이를 미분을 통해 최소화 할 수 있습니다.

$\begin{align} RSS &= (y-Xw)^T (y-Xw) \\ &= (y^T - w^TX^T)(y - Xw)  \\ &= y^Ty - y^TXw - w^TX^Ty + w^TX^TXw \end{align}$

 

이제 RSS를 w에 대하여 미분하여 그 값이 0 이되는 값을 구하면, 최소를 구할 수 있겠습니다. 

$\begin{align} {\partial RSS \over \partial w} &= -2X^Ty + (X^TX + X^TX)w \\ &= -2X^Ty + 2X^TXw \end{align}$

 

이 0이 되게 하면, $X^Ty = X^TXw$ 이므로 이때  $w = (X^TX)^{-1} X^Ty$ 입니다. 

참고로 행렬/벡터미분을 이용했습니다. 

또한 $(X^TX)$ 이 역행렬을 가져야 하고(full-rank, col row가 independent..등등) 이고, RSS의 w에 대한 헤시안 행렬 (2번 미분한 값) 이 0보다 커야(positive definite) 최소를 가지게 됩니다. 즉, ${\partial^{2} RSS \over \partial w^2} = (X^TX) > 0$ 여야 합니다.  

 

이번에 실제로 철수의 예제에 대하여 $w_0, w_1$ 을 구해봅시다. 위에서 구한 공식에 따라, 

 

import numpy as np

y = np.array([90, 80, 50, 20])
X = np.array([[1, 10], [1, 9], [1, 3], [1, 2]])
w = np.linalg.inv(X.T @ X) @ X.T @ y
print(w)

 

다음 과 같은 결과를 얻습니다. 

 

[15.6  7.4]

 

그러면, h(x) = 15.6 + 7.4x 를 얻을 수 있고, h(x) > 70 인 값을 얻기위한 공부시간 x는 

 

min_study_time = (70 - w[0]) / w[1]
print(min_study_time)

 

결과는 

 

7.351351351351353

 

이므로 OLS에 따라서는 철수는 적어도 7시간 30분 정도는 공부를 해야 하겠네요 😂😂

---

GD(Gradient Descent)

 

철수는 믿을 수 없었습니다. 8시간에 가까운 공부를 해야하다니!!

그래서 이번에는 GD(경사하강법)으로 H(x)를 구해보도록 했습니다. 

 

경사하강법이란 다음 수식으로 parameter 들을 구하는 것 입니다. 

 

$\theta = \theta - \eta \nabla_{\theta}L( H_{\theta} (x), y)$

 

loss(cost function) 에 대한 각 parameter들의 gradient 를 구해서 작아지는 방향으로 $\eta$ 만큼씩 업데이트 하여 이상적인 H(x)를 구하는 반복적 최적화 방법입니다. 일차 미분을 이용하고, parameter 의 해가 없는 경우나 아주 많은 경우에서도 실행 할 수 있는 장점이 있습니다. 

 

이번에는 $\theta$ 로 $H(x)$ 를 표현 해 보겠습니다. $H(x) = \theta_0 + \theta_1 x$

 

def hypothesis(theta_0, theta_1, x_data):
  return theta_0 + theta_1 * x_data

 

그리고 data를 setting하고 분포를 보겠습니다.

 

import numpy as np
import matplotlib.pyplot as plt

data = np.array([[10, 90], [9, 80], [3, 50], [2, 20]])

x_data = data[:, 0]
y_data = data[:, 1]

plt.figure(figsize=(8, 8))
plt.scatter(x_data, y_data, alpha=0.3, color='k')
plt.show()

 

 

plot data

 

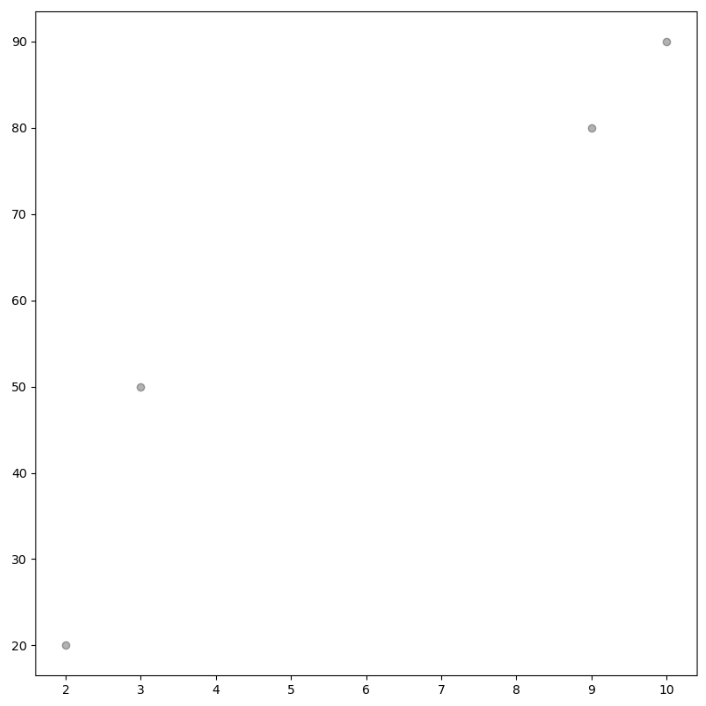
이번에는 Loss 를 보겠습니다. 

$L = \frac{1}{m}\sum_{i=1}^m{(H(x^i)-y^i)^2}$ 으로 두었는데, 미분의 편의성을 위해서 분모에 2m 을 넣으면 다음과 같습니다.

 

def l2_loss (h, y_data):
  m = len(h)  
  ret = np.sum((h-y_data)*(h-y_data)) / (2*m)
  return ret

 

$L = \frac{1}{2m}\sum_{i=1}^m{(H(x^i)-y^i)^2}$ 그리고 $\nabla L_{\theta}$ 는 모든 theta들에 대하여 각각 Loss를 미분한 것을 뜻합니다. 우리의 예제에서는 $\theta_0$ 과 $\theta_1$ 에 대한 각각의 미분값들 입니다. 

따라서 $ {\partial L \over \partial \theta_0} = \frac{1}{m} \sum ((\theta_0 + \theta_1 x) - y)$ 이고 ${\partial L \over \partial \theta_1} = \frac{1}{m} \sum (((\theta_0 + \theta_1 x) - y) \times x)$ 입니다, 그것들을 통해 업데이트를 하는 Gradient descent 코드는 다음과 같습니다. learning rate $\eta$는 0.01입니다.   

 

def gradient_descent(x, y, theta_0, theta_1, learning_rate=0.01):
  m = len(x)  
  gradient_theta_0 = np.sum(hypothesis(theta_0, theta_1, x) - y) / m
  gradient_theta_1 = np.sum((hypothesis(theta_0, theta_1, x) - y) * x) / m

  new_theta_0 = theta_0 - learning_rate * gradient_theta_0
  new_theta_1 = theta_1 - learning_rate * gradient_theta_1
  return new_theta_0, new_theta_1

 

각 parameter 들을 -30 (임의의 값) 으로 초기화(initialization) 한 후 업데이트 하는 코드는 다음과 같습니다. 

 

# initialize thetas as -30 each.
theta_0 = -30
theta_1 = -30

theta_0_list = []
theta_1_list = []
loss_list = []

# until converge about 10000 steps
converge_step = 10000
for i in range(converge_step):
  h = hypothesis(theta_0, theta_1, x_data)

  loss = l2_loss(h, y_data)
  loss_list.append(loss)

  theta_0_list.append(theta_0)
  theta_1_list.append(theta_1)
  theta_0, theta_1 = gradient_descent(x_data, y_data, theta_0, theta_1)
  
print(theta_0)
print(theat_1)

 

이렇게 10000번의 iteration 이후의 theta_0 과 theat_1 의 값을 보면 다음과 같은 값을 얻을 수 있습니다. 

이 값은.. 앞에서 OLS(최소제곱법) 으로 얻은 값 [15.6, 7.4] 과 매우 유사한 값을 구할 수 있습니다. 

 

15.599999999630178
7.400000000045993

 

그러면, h(x) = 15.599999999630178 + 7.400000000045993x 를 얻을 수 있고, h(x) > 70 인 값을 얻기위한 공부시간 x는 이때도 7시간 반 이상이었습니다. 철수는 과연 포기할까요? 순순히 8시간을 공부할 것일까요? 🤬

---

MLE(Maximum Likelihood Estimation)

 

마지막으로 철수는 한번 만 더 검증을 해 보기로 했습니다. 이번에는 (MLE) maximum likelihood estimation 이라는 방법으로 내가 공부해야 할 시간을 정확하게 알아보겠다는 열정에 사로잡힙니다. 

 

먼저 이를위해 확률(probability)과 가능도(likelihood)의 차이를 간단히 알아보겠습니다. 🤪

먼저 확률은 이산확률분포(discrete probability distribution)과 연속확률(continuous probability)로 나눌 수 있으며, 이산확률은 주사위의 한 면이 나오는 확률을 뜻하는 것 처럼 전체의 사건이 유한한(셀 수 있는)사건들로 이루어져 있고, 각각의 사건들의 확률을 구할 수 있는 분포 입니다. 여기서는 확률과 가능도가 같습니다. 

다음은 연속확률분포(continuous probability distribution)은 특정 확률분포가 주어지고, 각 사건의 확률은 0이고, 연속확률분포의 구간에 따른 확률분포에서 차지하는 영역(area under pdf)이 그 사건에 대한 확률이 되는 분포 입니다. 

 

확률은 probability density function 이 고정되었을 때, 그 차지하는 영역입니다. 고정되었다는 것은 그 확률분포를 구성하는 모수(parameter) 가 특정되었다는 것 입니다. 예를들어, 가우시안 분포는 $\mu, \sigma$ 의 함수로 나타낼 수 있습니다. 

 

$\mathcal{N}(\mu, \sigma^{2}) = \frac{1}{\sigma \sqrt{2\pi}} exp{(-\frac{(x-\mu)^{2}}{2\sigma^2})} $ 여기서 $\mu, \sigma$ 가 고정될 때 확률을 구할  수 있습니다.  

 

그러나 가능도(likelihood)는 data가 고정된 상태로 확률분포의 parameter 의 함수로 나타낼 수 있습니다. 즉 $p(X(고정)|\theta)=\mathcal{L}(\theta|X(고정))$ 입니다. 이는 그냥 그 사건에 대한 pdf 값으로 나타내면 됩니다.

 

철수에 예를 적용해 봅시다. 철수가 가지고 있는 시간(hour)과 점수(score)의 관계가 다음과 같은 수식으로 표현 할 수 있다 하겠습니다. $y = ax + b + \epsilon \sim N(0, \sigma)$ 즉, 위에서 예를 들었던 정규분포(mean=0, std=$\sigma$)를 따른다고 하겠습니다. $\epsilon = (ax + b) - y$ 입니다. (x, y) 값이 각각 (2, 20), (3, 50), (9, 80), (10, 90) 이 있고 이것을 가능도 함수에 넣어보면 각각의 likelihood(가능도)는 다음과 같습니다.  $\mu = 0$ 이고 $\epsilon$ 이 정규 분포를 따르므로 원래 pdf에서 x자리에 $(ax + b) - y$ 를 넣어 줄 수 있습니다.

 

$p(20|a, b, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} exp{(-\frac{((2a + b)-20)^{2}}{2\sigma^2})}$

$p(50|a, b, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} exp{(-\frac{((3a + b)-50)^{2}}{2\sigma^2})}$

$p(80|a, b, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} exp{(-\frac{((9a + b)-80)^{2}}{2\sigma^2})}$

$p(90|a, b, \sigma^2) = \frac{1}{\sigma \sqrt{2\pi}} exp{(-\frac{((10a + b)-90)^{2}}{2\sigma^2})}$

 

표본들의 전체의 가능도는, 각각의 표본들이 독립이라는 가정하에 모두의 곱으로 나타낼 수 있고, 계산의 편의성을 위해서 각 likelihood에 log를 취한 log likelihood를 최대화하는 $a, b$를 미분을 통해서 구할 수 있습니다. 

 

$log(likelihood) = log(p(20|a, b, \sigma^2)) + log(p(50|a, b, \sigma^2)) + log(p(80|a, b, \sigma^2)) + log(p(90|a, b, \sigma^2))$ 입니다. 이를 풀어서 쓰면, $log(\frac{1}{\sigma \sqrt{2\pi}}) * 4 + ((-\frac{((2a + b)-20)^{2}}{2\sigma^2}) + (-\frac{((3a + b)-50)^{2}}{2\sigma^2}) + (-\frac{((9a + b)-80)^{2}}{2\sigma^2}) + ((-\frac{((10a + b)-90)^{2}}{2\sigma^2}))$ 입니다. 

 

이제 이를 최대화 하기 위해 각각 a, b 에 대하여 미분을 하면, 

${\partial log(likelihood) \over \partial a} = \frac{(388a + 48b - 3620)}{-2\sigma^2}= 0$ 이고,

${\partial log(likelihood) \over \partial b} = \frac{(48a + 8b - 480)}{-2\sigma^2} = 0$ 입니다. 

이 연립방정식을 풀어보면, 

 

a = 7.4, b = 15.6 이 나오고 위의 값들과 일치합니다. 😎😎

---

철수는 이제 포기하고 공부를 시작하려 했습니다. 적어도 8시간은 해야겠지요.

그러나 검증을 하느라 시험공부시간이 1시간도 채 안남았다고 하네요.. 

결국에는 게임기를 얻지 못한 슬픈 결과가 나왔답니다. 😂😂😂😂😂😂

 

이번 포스팅은 예를들어서 여러가지 방법으로 선형회귀를 풀어보는 시간을 가졌습니다. 

질문과 토론 그리고 오타등 댓글은 환영합니다. 

감사합니다 뿅! 👏

 

 

Reference

https://ko.wikipedia.org/wiki/%ED%9A%8C%EA%B7%80_%EB%B6%84%EC%84%9D

https://ko.wikipedia.org/wiki/%EC%84%A0%ED%98%95_%ED%9A%8C%EA%B7%80​

https://datascienceschool.net/02%20mathematics/04.04%20%ED%96%89%EB%A0%AC%EC%9D%98%20%EB%AF%B8%EB%B6%84.html

https://statproofbook.github.io/P/slr-mle

https://ko.d2l.ai/chapter_deep-learning-basics/linear-regression.html