[Theme 05] MLE (Maximum likelihood estimation) 을 통한 Loss

안녕하세요 pulluper 입니다! 😀 저번까지 linear regression, logistic regression, softmax regression 등의 개념을 살펴보았는데요. 머신러닝공부를 하다보면 나오는 심심찮은 개념인 MLE 이름은 익숙한데, 실제 개념이 헷갈리시다면 이번 포스팅을 잘 읽어보시기 바랍니다! 이번 시간에는 MLE의 개념과, 이를통해서 만들어지는 Loss의 특징들에 대하여 알아보겠습니다. 목차는 다음과 같습니다.

 

1. Likelihood (bayes' rule)
2. MLE
3. Negative Log Likelihood
4. Examples

먼저 bayesian rule 에 나오는 likelihood 와, MLE에 개념, 이를 Loss 로 사용하는 NLL, 그리고 task에 맞는 examples 들의 내용을 다뤄보겠습니다. 그럼 시작해보겠습니다 ~ 🎬

---

1. Likelihood (우도) 

 

Likelihood (우도) 의 개념은 Bayes' rule 에서 왔습니다. 이는 다음과 같습니다. 

 

$P(A|B)={\displaystyle \frac{P(B|A)P(A)}{P(B)}}$

 

이것이 뜻하는 바는, 조건부 확률은 집합의 교집합을 주어진 집합의 확률로 나누어 나타낼 수 있다는 것 입니다. 다음 그림을 보시면 이해가 쉽습니다. 마지막 부분으로 유도 될 때, 확률의 곱의 법칙이 사용 되었습니다. 

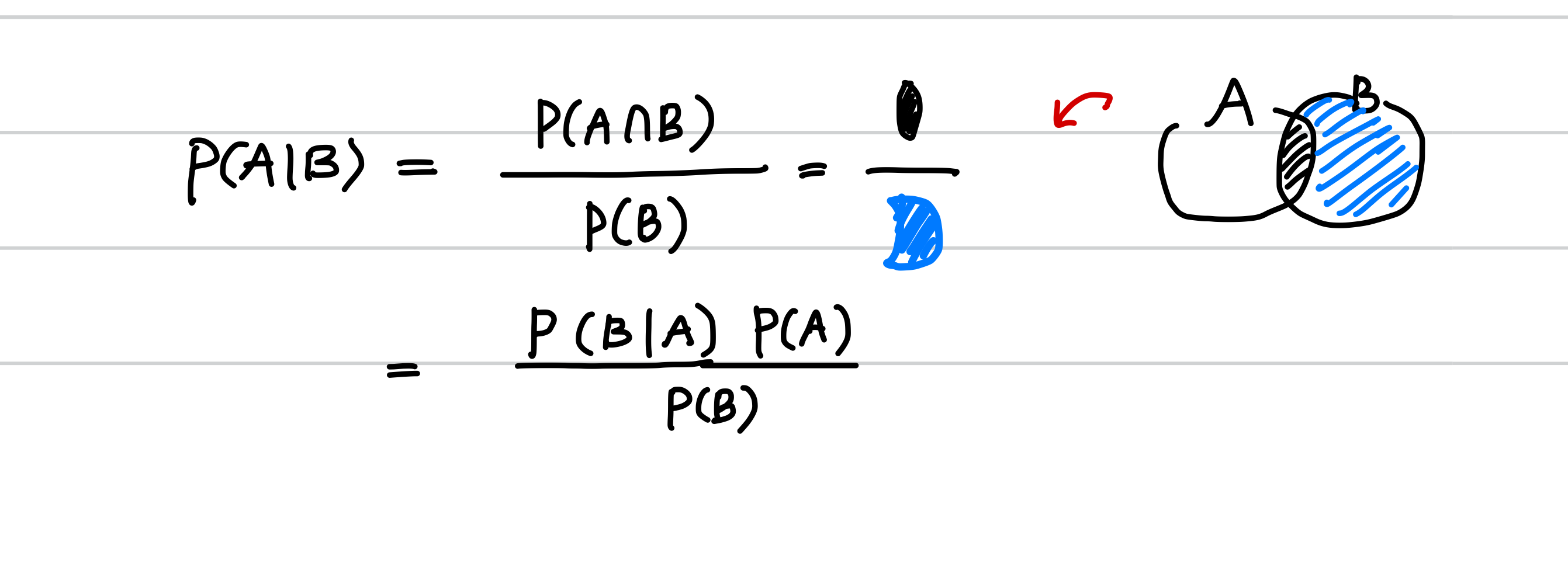
이 베이즈 정리에, 의미를 부여해 보겠습니다. 

 

$P(\theta |X)={\displaystyle \frac{P(X|\theta )P(\theta )}{P(X)}}$

 

$\theta$ : hypothesis로 추정하고자 하는 값 입니다. 이는 특정 클래스가 될 수도 있고, 확률분포의 모수가 될수도 있습니다. 

$X$ : observation로 관측된 데이터로 예를들어 training data 가 될 수 있습니다. 

$P(\theta )$ : prior probability 추정하려는값의 미리 가지고 있는 확률분포를 뜻합니다. 

$P(X)$ : marginal probability 혹은 evidence 이며, data X 자체의 분포를 뜻합니다. 

$P(\theta |X)$ : posterior probability로 X가 주어졌을 때의 $\theta$ 의 분포입니다. X의 영향을 받습니다. 

$P(X|\theta )$ : likelihood로 $\theta$ 가 주어졌을 때(가정을 한 상태)에서의 X의 확률분포입니다. 

 

제가 예전포스팅에서 다음과 같이 likelihood를 말했습니다. 

그러나 가능도(likelihood)는 data가 고정 된 상태로 확률분포의 parameter 의 함수로 나타낼 수 있습니다. 즉 $p(X(고정)|\theta )=\mathcal{L}(\theta |X(고정))$ 입니다. 이는 그냥 그 사건에 대한 pdf 값으로 나타내면 됩니다.

 

저도 포스팅을 하면서 갑자기 이부분이 혼동 되었었는데요. X가 고정이 되었다면, $P(\theta |X)$ 가 likelihood 의 의미가 되어야 하는것이 아닌가? 하는 의문이 들었습니다. 💦💦💦

 

이와 관련하여 개념을 정립하는데, 비슷한 질문이 다음에 있었습니다.

https://stats.stackexchange.com/questions/429819/what-is-the-conceptual-difference-between-posterior-and-likelihood?answertab=scoredesc#tab-top 

What is the conceptual difference between posterior and likelihood?

답변자는 다음과 같이 likelihood 의 의미를 말합니다. 

"만약 𝜃가 특정 값을 취한다는 것을 알았다면 우리가 가지고 있는 데이터를 관찰할 확률은 얼마나 될까요?"

 

다시 $P(X|\theta )$ 의 의미를 보면, $\theta$ 가 주어졌을때이지 고정된것은 아닙니다. 따라서 특정 분포를 취할때(정규분포등), 특정 X를 관찰할 확률이라고 생각하면 될 것 같습니다. 즉, 만약 observed 된 data X가 {2, 3, 4} 이고, 이들이 정규분포에서 나왔을 확률(likelihood)는 다음과 같습니다. 

 

$P(X|\theta )=P(X|\mu ,\sigma )$ 

 

이때, 각 data 들이 IID 조건을 만족한다고 하면, 

 

$\begin{array}{rl}P(X|\theta )& =P(X|\mu ,\sigma )\\ & =P(2|\mu ,\sigma )\times P(3|\mu ,\sigma )\times P(4|\mu ,\sigma )\\ & =\prod _{i=1}^{n}P(x_i|\mu ,\sigma )\\ & =\prod _{i=1}^n{\displaystyle \frac{1}{\sqrt{2\pi {\sigma }^2}}}ex{p}^{-\frac{(x_i-\mu {)}^2}{2{\sigma }^2}}\end{array}$

 

 

따라서 결국 위에서의 likelihood $P(X|\theta )$ 는 $\mu ,\sigma$ 의 함수가 되면서 data들의 "그 분포의 PDF들의 곱" 으로 표현할 수 있습니다. 즉, 특정 분포의 곱으로 가정하는것을 기억해 두시면 됩니다. 👏👏👏👏👏

---

2. MLE(Maximum likelihood estimation)

 

우리의 목표는 Posterior 를 최대화 시키는 것 입니다. 왜냐하면, $P(\theta |X)$ 가 커질때, $P(\theta )는$ 보통 1로 두기 때문입니다. 즉, X라는 data 가 주어졌을 때 $\theta$ 라는 가설이 맞을 확률을 늘리는 $\theta$ 를 찾아야 하기 때문입니다.  그렇다면, 어떻게 Posterior를 최대화 할 수 있을까요? 위의 베이즈 법칙에 의하여 posterior 는 prior 와 비례함을 알 수 있습니다. 

$P(\theta |X)={\displaystyle \frac{P(X|\theta )P(\theta )}{P(X)}}\propto P(X|\theta )$

 

posterior 를 정확히 구하기 위해서는 prior 를 알아야 합니다. 근데 이게 어렵습니다. 따라서 likelihood를 최대로 만드는 방법으로 posterior 를 최대화 시키도록 근사하여 $\theta$ 들을 구하는 것이 바로 MLE입니다.  

 

예를들어 보면 위에서 data = {2, 3, 4} 에 대한 likelihood 는 $\mu ,\sigma$ 에 대한 함수인데, 이를 최대화 시키는 각각의 $\mu ,\sigma$ 를 구하는 것입니다. 어떻게 구하냐면, 이제 최적화 문제가 되었으므로 미분을 이용하거나, Gradient Descent 방법등을 이용합니다.

---

3. Negative Log-Likelihood

 

네 좋습니다 이제 우리는, likelihood 를 최대화 시키면 됩니다! 그런데 왜 log likelihood 를 사용할까요? 그것은 다음 질문에서 알 수 있었습니다. [link]

 

바로 곱하기 연산을 덧셈으로 바꿀 수 있기 때문입니다. 아래 그림과 같이 Likelihood는 곱으로 표현이 되는데 log 를 취하면, 덧셈으로 표현 가능합니다.   

product -> sum

또한 아래와 같이 gaussian, bernoulli 등의 분포에 포함된 exponential 에 대한 계산을 피할 수 있기 때문입니다. 

get rid of exponential computations

 

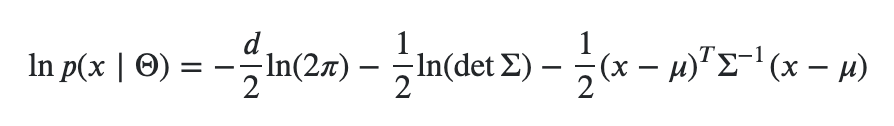
그리고 log 함수는 단조증가 함수이기 때문에, likelihood에 연산을 하여도 그 순서등의 관계를 바꾸지 않습니다.  

마지막으로 Negative는 음수를 곱해줘서 Maximum 문제를 Minimum 문제로 바꾸기 위한 목적입니다. 

 

정리하자면, 만약 우리가 GD 로 이 문제를 풀어야 합니다. 그런데, 가정한 모델이 exponential 과 곱으로 구성되어 있다면, 곱의 미분등을 모두 구해야 하는데 이렇게 되면 computational cost가 매우 커지게 됩니다. 이를 방지하기 위해 더 간단하게 연산 할 수 있는 log likelihood 를 사용합니다. 

---

4. Examples

 

이제 Likelihood 에 대한 예를 2가지 들어보겠습니다. X가 주어졌을때, deep neural network 를 통한 Y에 대한 likelihood 는 다음과 같습니다. 

$\begin{array}{rl}P(Y|X)& =P(Y|w=f_{\theta }(X))\\ & =P(Y|X;\theta )\end{array}$ 

 

1. Let Y ~ gaussian, $\mu =f_{\theta }(X),\sigma =1$ 이라 가정하면, 

 

Then, Likelihood  $=\prod _{i=1}^n\frac{1}{\sqrt{2\pi }}{e}^{-\frac{(y_i-f_{\theta }(x_i){)}^2}{2}}$

 

Negative Log Likelihood : 

$\begin{array}{rl}& =-\sum _{i=1}^n\{ln\frac{1}{\sqrt{2\pi }}-\frac{1}{2}(y_i-f_{\theta }(x_i){)}^2\}\\ & =\sum _{i=1}^n\{\frac{1}{2}(y_i-f_{\theta }(x_i){)}^2+const\}\end{array}$

이는 Sum Square Error 와 같습니다. 

 

2. Let Y ~ Bernoulli, $p=f_{\theta }(X)$ 이라 가정하면,

 

Then, Likelihood $=\prod _{i=1}^n{f}_{\theta }(x_i{)}^{y_i}(1-f_{\theta }(x_i){)}^{(1-y_i)}$

 

Negative Log Likelihood : 

$\begin{array}{r}=-\sum _{i=1}^n\{y_{i}ln(f_{\theta }(x_i))+((1-y_i)ln(1-f_{\theta }(x_i)\}\end{array}$

이는 Binary Cross Entropy 입니다.

 

Y가 multi normial distribution 을 사용한 예는 다음 포스팅에 있습니다.  https://csm-kr.tistory.com/48

[Theme 04] Multinomial Logistic Regression (Softmax Regression)

 

MLE 를 통해서 NLL loss 의 예를 보았는데, 우리가 익숙했던 loss 가 나오니 신기하지 않나요? 이렇듯, Y가 continuous 한 성질을 가진다면 가우시안 분포로, Y가 2개의 클래스를 가질것 같다면 베르누이 분포로 가정하여 MLE를 이용 할 수 있습니다. 각각은 regression, classification 문제를 푸는데 적절합니다.  

 

---

네 이번 포스팅은 MLE 에 대하여 알아보았습니다. 마지막으로 복습을 위한 quiz 를 보고 포스팅 마치겠습니다. 

1. bayes's rule 에 대한 설명을 하시오

2. likelihood 의 의미를 설명하세요. 

3. MLE 가 NLL 을 쓰는 이유를 설명하세요. 

4. Y가 gaussian 일 때, deep nueral net $p(Y|X)$ 의 loss 가 SSE 가 됨을 보이세요. 

 

다음에는 XOR, MLP 에 대하여 포스팅 할 예정입니다. 감사합니다.  😎😎😎😎😎

---

Reference 

 

https://sanghyu.tistory.com/10

https://stats.stackexchange.com/questions/429819/what-is-the-conceptual-difference-between-posterior-and-likelihood

https://math.stackexchange.com/questions/892832/why-we-consider-log-likelihood-instead-of-likelihood-in-gaussian-distribution

https://hwiyong.tistory.com/27

https://www.youtube.com/watch?v=o_peo6U7IRM&t=2977s