[Object Detection] FreeAnchor: Learning to Match Anchors for Visual Object Detection (NIPS2019)

안녕하세요! pulluper 입니다. 오늘은 NeurIPS 2019 에 발표된 FreeAnchor 에 대하여 리뷰해보는시간을 가져보겠습니다!

저자는 Xiaosong Zhang 등 5분으로 object detection 을 하셨던 분들입니다. 

이 paper 의 가장 큰 특징은 MLE의 관점으로 object detection 을 제안했다는 것입니다. 

---

먼저 MLE 에 대하여 알아보겠습니다.

 

likelihood 

이를 위해 likelihood 에 대하여 알아보겠습니다. 

위키피디아에 likehood 에 대하여 찾아보면 다음과 같이 나옵니다.

 

In statistics, the likelihood function (often simply called the likelihood) measures the goodness of fit of a statistical model to a sample of data for given values of the unknown parameters.

 

통계학에서, $\theta$ 에 대한 확률분포 $D_{\theta}$ 가 있다고 합시다, 

그런데 observation(관측치) 가 주어졌을때, 그 관측치들이 확률분포와 얼마나 일치하는가를 나타내주는 함수입니다. 

이는 $L(\theta|X)$ 로 표현이 됩니다. 

X가 특정 분포로부터 만들어졌을 확률입니다. (사실 확률은 아닙니다.)

 

likelihood 설명

---

MLE

MLE란? maximum likelihood estimation 의 줄임말로, likelihood 를 가장 크게하는 estimation 방법입니다. 

즉, 위에서처럼 observation $X = \{x_1, x_2, ..., x_n\}$ 와 $D_{\theta}$ 가 주어졌을때, 주어진 표본들로부터 가능도(likelihood)를 가장 크게하는 $\theta$ 추정하는 방법입니다. 

다음이 MLE 의 목표가 됩니다.

$\hat{\theta} = argmax_{\theta} L(\theta|X)$

 

확률분포 $D_{\theta}$ 에 대하여 관측치(observation) X 가 i.i.d(independent and identically distributed) 조건을 만족한다면, $L(\theta|X) = \prod_i D_\theta (x_i)$ 로 표현을 할 수 있습니다. 

 

---

Loss formulation 

그리고 이 논문에서는 기존의 object detection 에 대한 loss 를 종합적으로 재구성합니다. 

다음과 같이 anchor 를 사용하는 object detection 의 general 한 loss 를 분석합니다.

formulation of object detection loss

여기서 A, B, C 가 뜻하는 바를 알아보겠습니다. 

먼저 A 는 a set of anchor boxes, B는 a set of ground truth boxes 입니다. 아래 그림과 같이 표현 할 수 있습니다. 

A : set of anchors / B : set of gt bounding box

보통의 anchor based object detection 은 A 와 같이 pre-defined 된 다수의 anchor boxes 를 이용합니다. 그 anchor 들로부터 gt 를 찾도록 합니다. 그럼 여기서 각 anchor 가 학습할 가치가 있는지 아닌지를 판단하는 것은 anchor 와 gt 의 iou 에 따라서 입니다. 이는 C 에서 설명 할 수 있습니다. 

C는 matching constant 를 뜻합니다. 

 

matching constanct

만약 어떤 threshold T 보다 값이 그면 1 그렇지 않다면 0을 할당합니다.  

그렇데 되어 positive anchor 는 1 을 할당하고 negative anchor 는 0 을 할당합니다. 따라서 학습과정에서 positive anchor 만이 학습에 참여하게 되므로, 네트워크는 object 가 있는 부분부터 학습에 영향을 끼치게 됩니다. 

 

다시 전체 loss 를 보면

formulation of object detection loss

loss 는 classification 부분과 box regression 부분 그리고 background 를 판단하는 부분으로 나타낼 수 있습니다. 

---

Loss as MLE perspective 

 

이번에는 detection loss 를 MLE 관점으로 해석을 하는 부분을 보겠습니다. 

먼저 위의 detection loss 를 -exponential 을 취합니다. 

그렇게 되면 더하기는 곱하기로 바뀌고 다음과 같은 식으로 전개 할 수 있습니다. 

이제, P 를 MLE 의 관점으로 해석 할 수 있습니다. 

-exponential 을 취했기 때문에, 각 anchor 들에 관한 합은 곱하기로 변하게 되고, 이를 하나의 Likelihood 들의 곱으로 해석하면, 이것을 줄이게 되는것은 likelihood 를 줄이는 MLE 방식으로 볼 수 있습니다. 

---

NMS and Anchor bag

NMS and Anchor bag

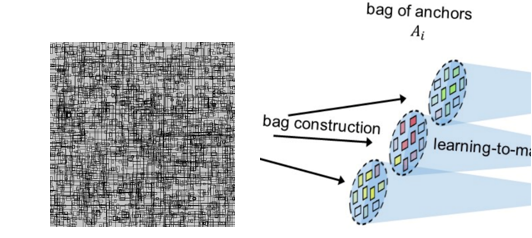
그리고 이 논문의 또 하나의 특성은 object detection 의 evaluation metric 인 recall 과 precision 의 개념을 anchor bag 에서 anchor 를 찾는데 사용한다는 것 입니다. 

 

먼저 Recall 에 대하여 보겠습니다. recall 이란 

recall

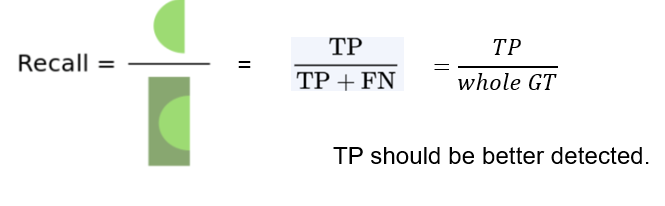
Recall 은 True positive 를 True positive + False negative 로 나눈 것 입니다.

즉, 전체 정답중에 모델이 맞춘것의 비율입니다. 

이 개념을 사용하여 recall 을 높이기 위해서는 True positive 가 크게되면 recall 이 커지게 됩니다. 

p recall

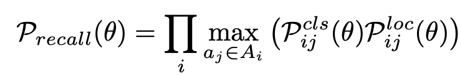
따라서 위의 식과같이 recall 이 커지게 하는 anchor 를 anchor bag 에서 찾도록 합니다. recall 을 최대화하는 방향의 anchor 를 P_recall 이라 정의하고 이를 loss 에 사용합니다. 

 

이번에는 Precision 입니다. 

 

precision

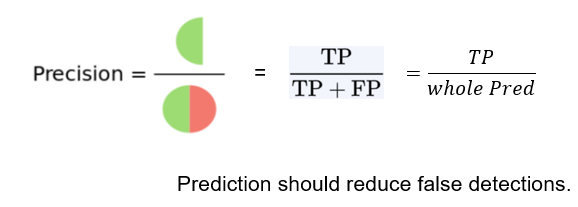
Precision 은 TP /  TP + FP 인데, 전체 네트워크의 정답중에서 얼마나 맞는지를 판단하는 것 입니다. 이를 높이기 위해서는 false postive 가 낮아지면 됩니다. 

p precision

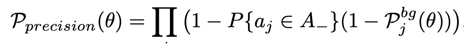
다음과 같은 식을 사용하면, precision 을 높이는데 도움이 되는데 중간의 $p\{a_j \in A_{-}$ 는 saturated linear 로 다음과 같은 식입니다. 

saturated linear

결국 두 개념을 모두 사용한 loss 는 다음과 같이 확장 될 수 있습니다. 

custom likelihood

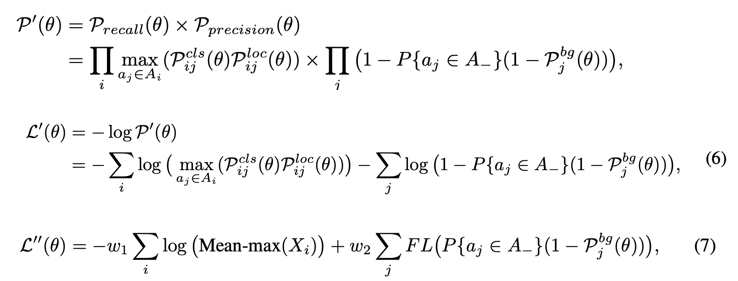
이는 논문에서 제안한 custom likelihood 이며, 이것을 줄이면, object detection 의 loss 와 함께 MLE 관점에서의 recall 과 precision 을 키우는 방향으로 학습이 됨을 내포합니다. 

 

Where Mean-max 함수는 다음과 같습니다. 

mean-max fn

---

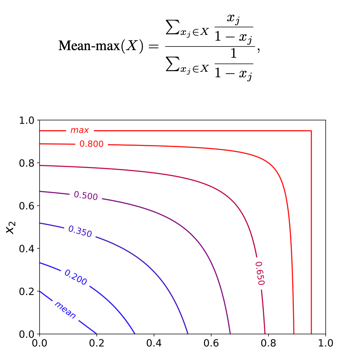
Experimental results

 

anchor bag training

 

그리고 기존의 네트워크에 add-on 하여 성능을 높이는데 도움이 됨을 볼 수 있었습니다.

 

quantitative result

 

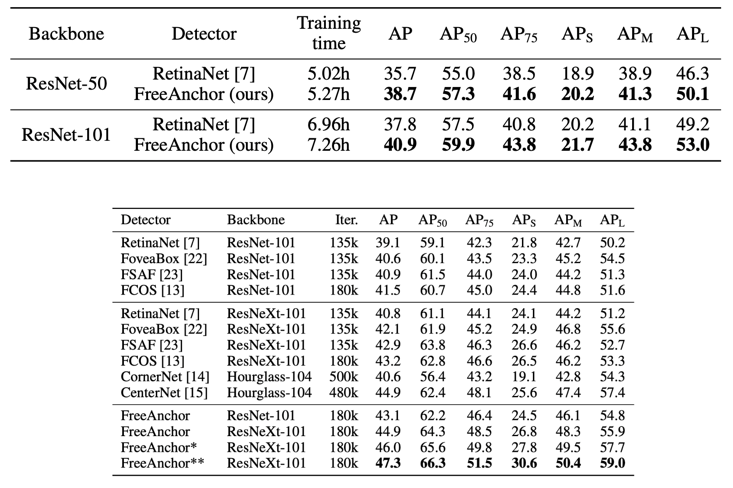
(작성중...)

 

Reference 

https://medium.com/@andersasac/anchor-boxes-the-key-to-quality-object-detection-ddf9d612d4f9

Anchor Boxes — The key to quality object detection

https://forums.fast.ai/t/deeplearning-lec9-notes/14113

DeepLearning-Lec9-Notes