안녕하세요 pulluper 입니다 :)
이번포스팅은 ECCV2020 에서 best paper를 받으며 Nerf 바람을 불러온
첫 논문 NeRF(Neural Radiance Fields for View Synthesis)에 대하여 알아보도록 하겠습니다.
https://arxiv.org/pdf/2003.08934.pdf
1. Preliminary
Camera Calibration
카메라의 이미지는 3차원 공간상의 점들을 2차원 평면 이미지로 투영시킨 것 입니다.
Camera Calibration이란, (핀홀)카메라 모델을 기준으로 3차원 혹은 2차원으로 변환할때의
그 내부 파라미터를 구하는 과정입니다. 다음 그림을 보시면 맨왼쪽 부터 오른쪽으로
Real Space(검정), normalized plane(빨강), image plane(파랑)을 볼 수 있습니다.
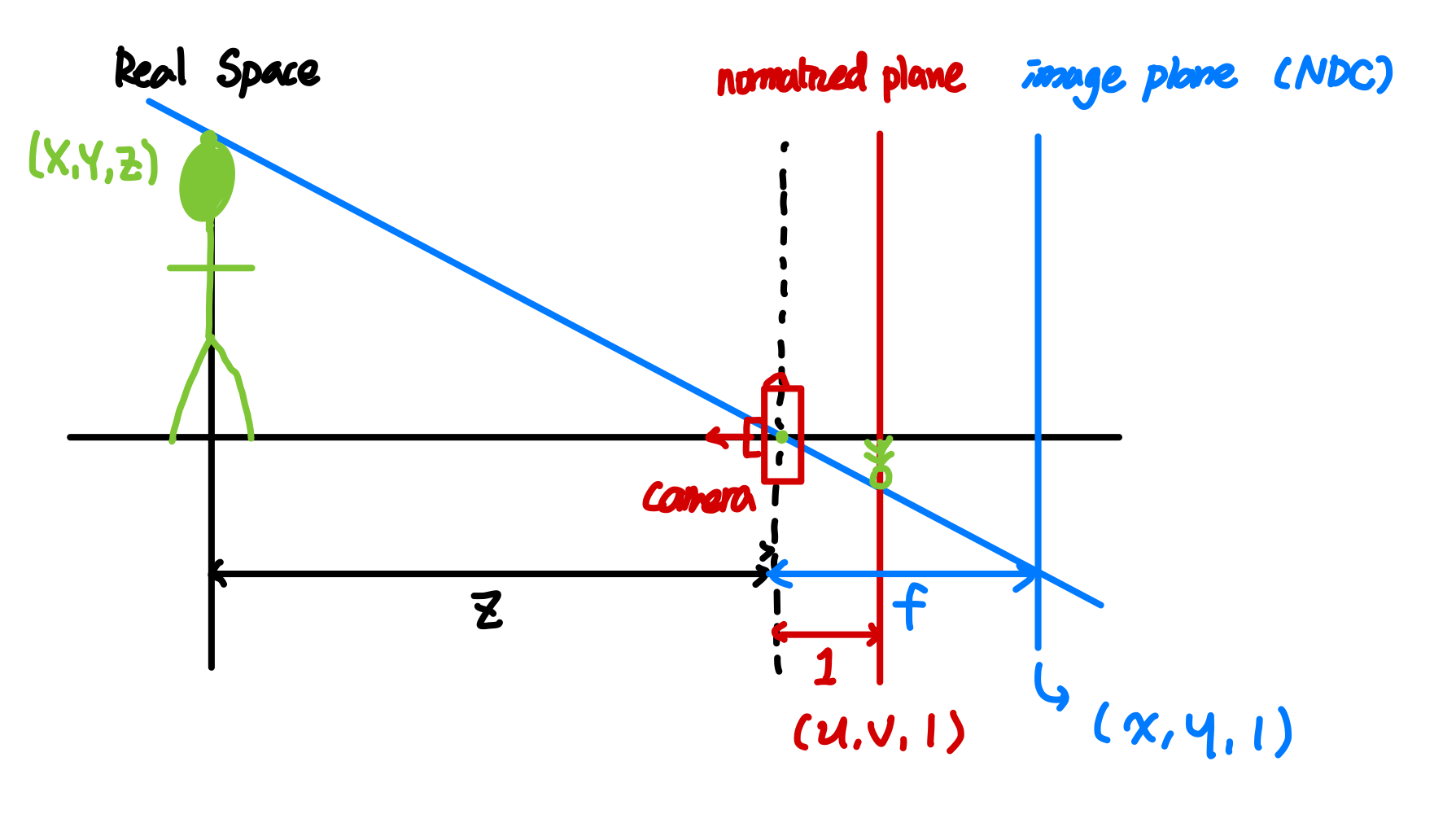
Real Space의 좌표 $(X, Y, Z)$ [초록색]에 사람이 한명 서 있다고 하겠습니다. 이 사람에 대하여,
카메라에 투영하기 위해서 Z값(깊이)를 1로 정규화 한 이미지가 맺히는 공간을
normalized plane이라고 하며, 이때, $(u, v, 1)$ 이라는 좌표값을 갖게 됩니다.
그리고 u, v 는 각각 비율에 의하여 X/Z, Y/Z 값을 가집니다. (카메라 앞쪽에 있어도 무방)
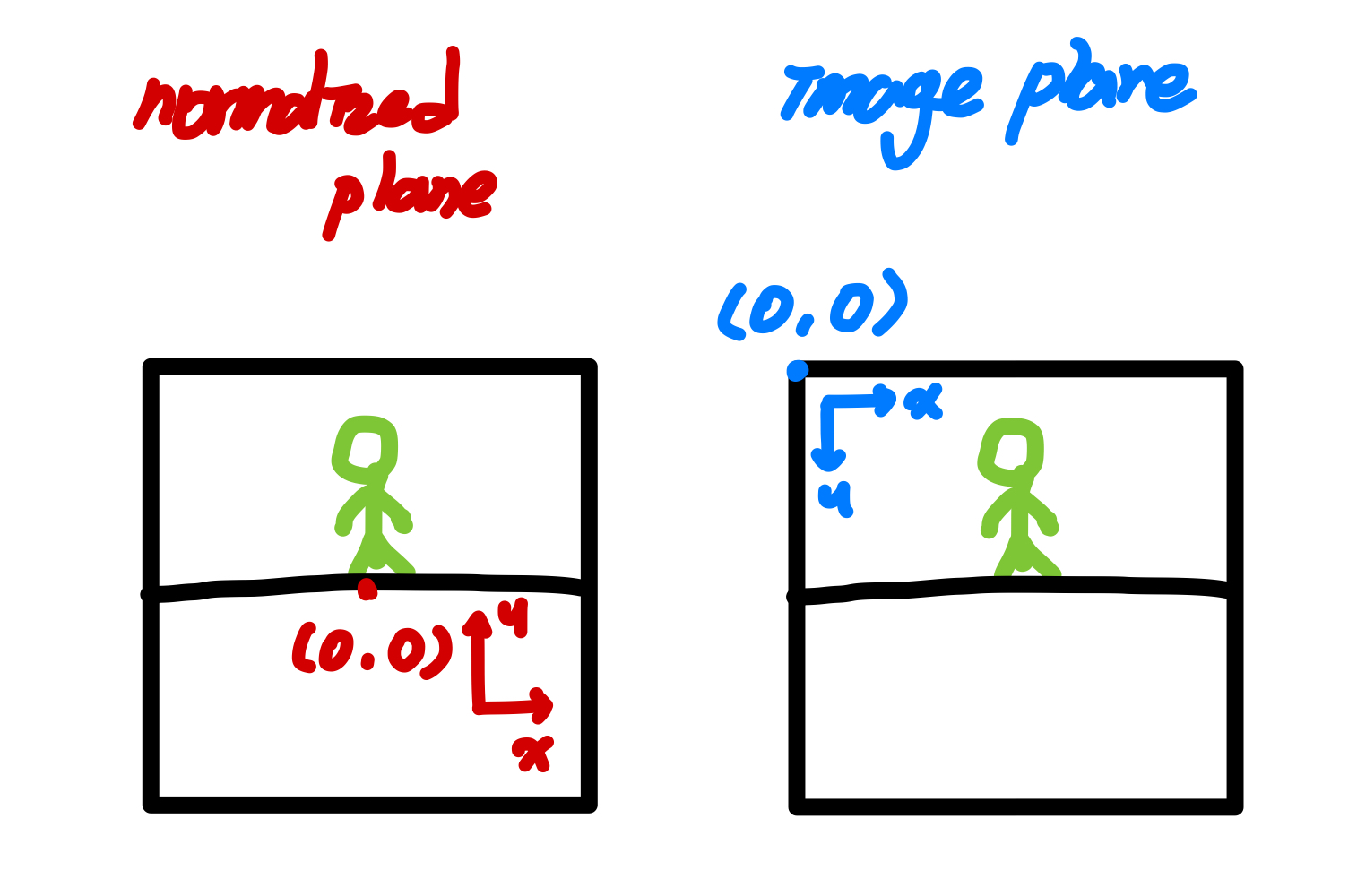
normalized plane 에서 맺힌 이미지를 image plane으로 변화시키기위해서는
아래 그림처럼 중심에 있는 원점을 오른쪽과 같이 좌상점으로 변경해 주어야 하고,
초점거리(fx, fy)를 각각 곱해주어 image plane 상의 pixel coordinates를 만듭니다.
따라서 (x, y, 1) = (u * fx + cx, v * fy + cy, 1) 이 되게 되고 이를 행렬로 나타내면 다음과 같습니다.
(여기서 cx, cy 는 보통 이미지 너비와 높이 W, H 의 반을 빼주는 값 입니다. 즉, (-W/2, -H/2))
$\begin{equation} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \end{equation}$ = $\begin{equation} \begin{pmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{pmatrix} \end{equation}$ $\begin{equation} \begin{pmatrix} u \\ v \\ 1 \end{pmatrix} \end{equation}$ ...................... (1)
(u, v, 1) 앞에 곱해지는 matrix 를 intrinsic matrix(K)라고 하고
이는 normalized plane 에서 image plane으로 변환 시켜주는 역할을 합니다.
또한 주목해야 할 점은 두 plane 의 y좌표의 방향이 다르다는 점 입니다.
이 사실은 Nerf에서 d (direction) 벡터를 구할 때 사용됩니다.
이번에는 그림 1 에서 만약 카메라가 보는 방향이 다음과 같이 변경이 되면 어떻게 될까요?

이렇게 되면, 다음과 같이 카메라의 fov의 시야만큼의 보이는 부분이 달라지고 이는 다시
카메라 내부에서 normalzed plane, image plane으로 맺히게 됩니다.
즉 카메라의 위치 혹은 방향이 달라지면, 이미지 자체도 달라지기 때문에
이 부분을 intrinsic matrix 보다 먼저 고려해 주어야 합니다.
이렇듯 카메라의 회전, 평행이동을 다룬 matrix를 extrinsic parameter 라고 하며
이를 고려한 식은 다음과 같습니다.
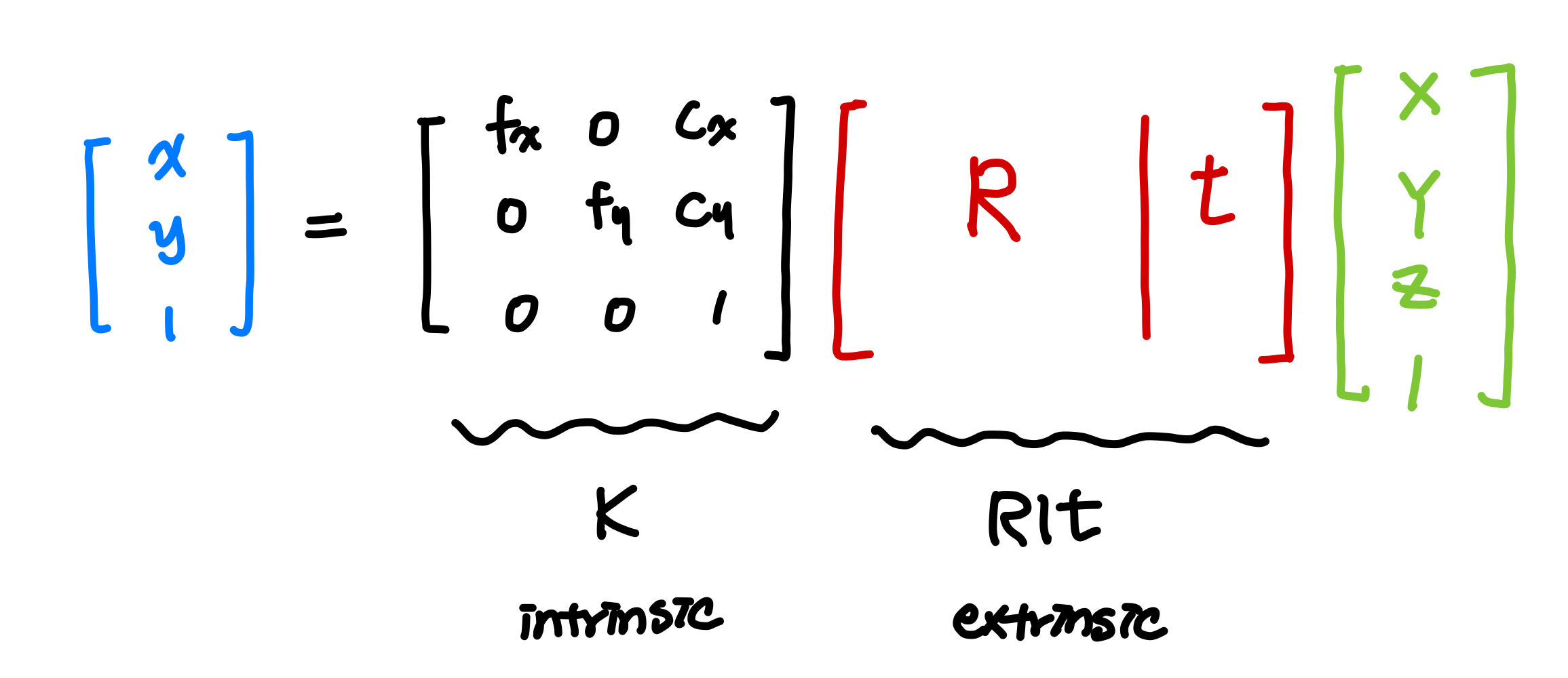
여기서 $R \in \mathbb{R}^{3 \times 3}$ 은 rotation matrix 이며, $t \in \mathbb{R}^3$ 는 translation matrix 입니다.
이렇듯, 3차원 좌표 [X, Y, Z] 가 이미지 좌표 [x, y] 로 변환될 때 내부의 모델 파라미터를 추정하는 방법을
camera calibration 이라 합니다.
2. NeRF
NeRF란 무엇일까요?
Neural Radiance Fields 즉, 뉴럴 네트워크를 통한 빛 방사장 입니다.
또한 뒤에 "for view synthesis" 라는 단어가 붙었습니다.
이는 새로운 시점 생성이라는 뜻으로 이해할 수 있겠네요.
아이디어의 스케치는 다음과 같습니다.
다음 그림을 보시면 왼쪽의 지정된 카메라의 위치에서 찍은 이미지로 학습하여
오른쪽의 파란색 카메라 위치의 새로운 시점에서 본 물체의 모습을 생성해 내는 것 입니다.


오른쪽의 파란색 카메라는 2개만 그려졌지만
자신이 만들어내고 싶은 모든 위치의 시점생성을 할 수 있습니다.
즉 discrete 한 이미지들로부터 에서 continuous한 시점을 생성 해 내고 싶은 것 입니다.
이를 위해서 NeRF에서는 Ray라는 개념을 사용했습니다.
3. Ray
Ray란 각 pixel들로부터 실세상(Real Space) 방향으로 뻗어 나가는 빛을 모델링 한 개념입니다.
이는 r(t) = o + t d 로 표현합니다.
여기서 o 는 카메라의 위치이고
d는 viewing direction으로 위 그림에서
normalized plane에서부터의 real space 방향의 벡터
$(u, v, 1)_* ^T$ 에 카메라의 회전을 적용한 벡터입니다.
먼저 d를 구하기 위해서 수식 (1)을 역변환 시킵니다.
이 작업은 pixel coordinate(Image plane) 에서 normalzed plane으로 변환 하는 작업입니다.
image plane 의 좌표 $(x, y, 1)^T$ 와 $(u, v, 1)^T$ 의 관계는 다음과 같이 표현됩니다.
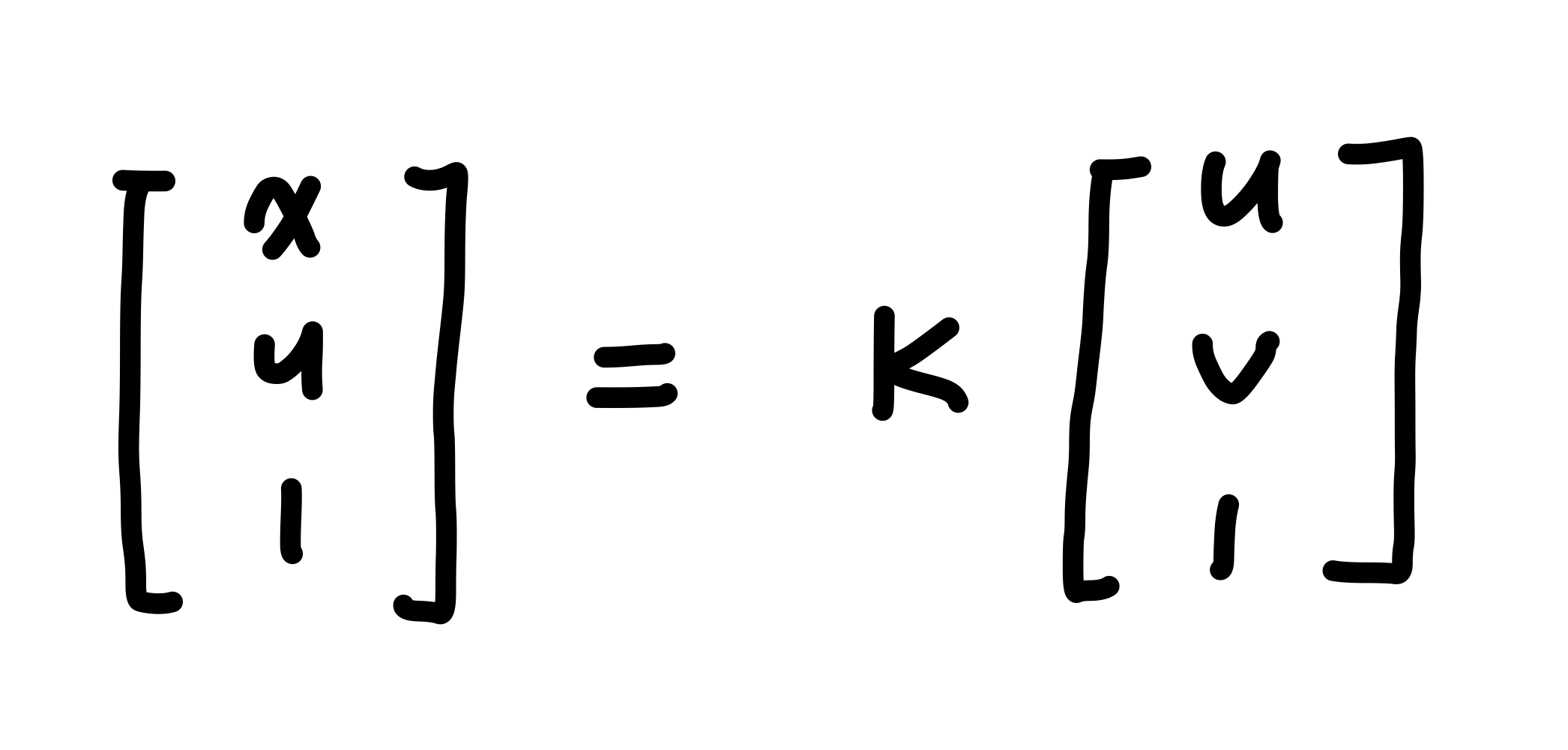
intrinsic parameter 인 K를 풀어쓰면 다음과 같습니다.
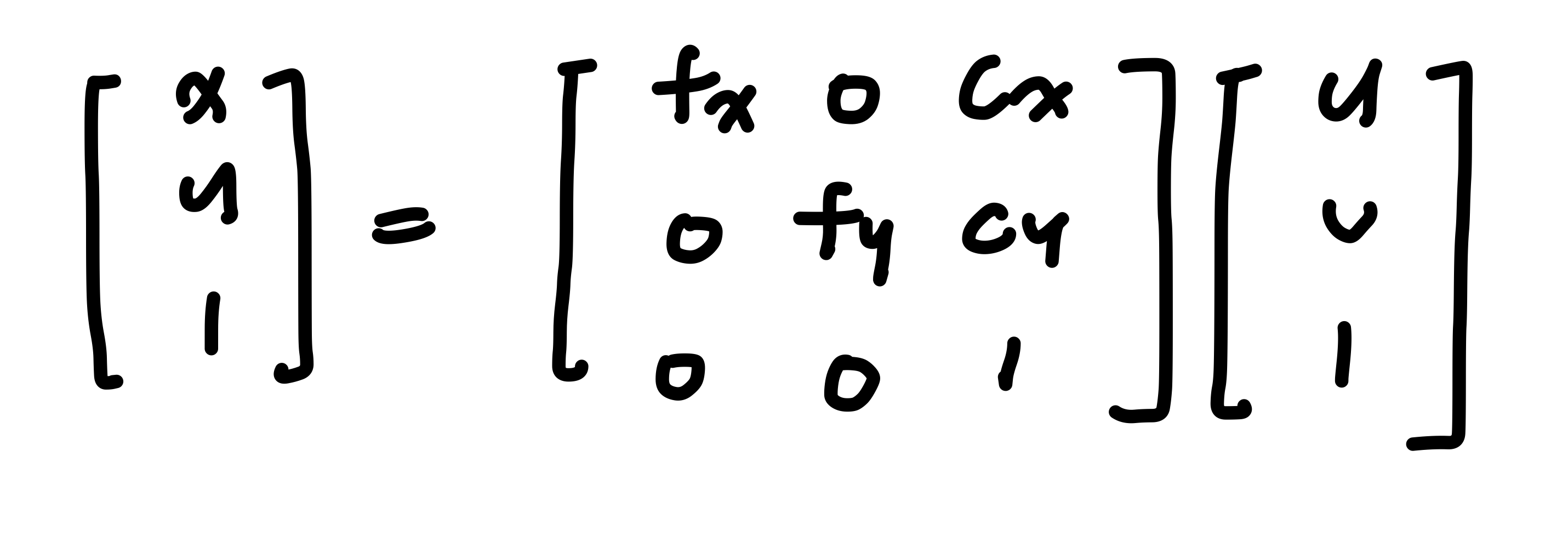
그리고 양변에 K의 역행렬을 곱해주면, 다음과 같이 $(x, y, 1)^T$ 에서 $(u, v, 1)^T$ 로 변환하는 식이 됩니다.
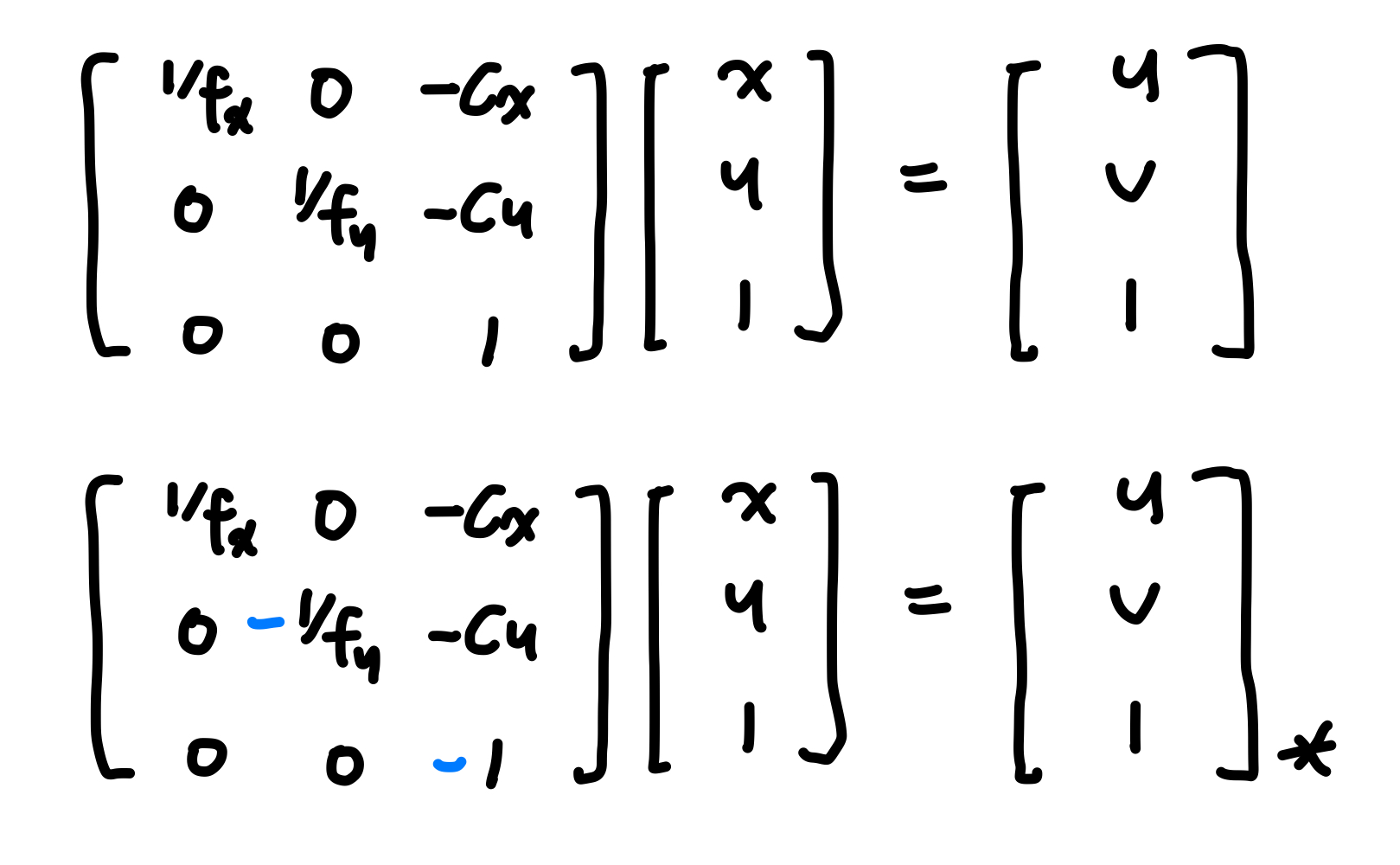
여기서 주목할 점은, 아래 수식의 $(u, v, 1)_* ^T$ 는 주대각성분 y, z 에 파란색으로 표시된 것처럼
부호변경이 있는 것 입니다.
그림 2에서와 같이 y축의 좌표는 반대가 되고, z축은 그림으로부터 실제 세상방향이기 때문에 축의 방향을
고려해서 다음과 같은 부호 변경이 존재합니다.
참고로 이때, fx와 fy는 같은 경우가 많은데, 데이터에서는 다음과 같이 camera_angle 등으로 표시됩니다.
이 angle (alpha) 를 통해 focal (fx or fy) 를 구하는 방법은 다음과 같습니다.
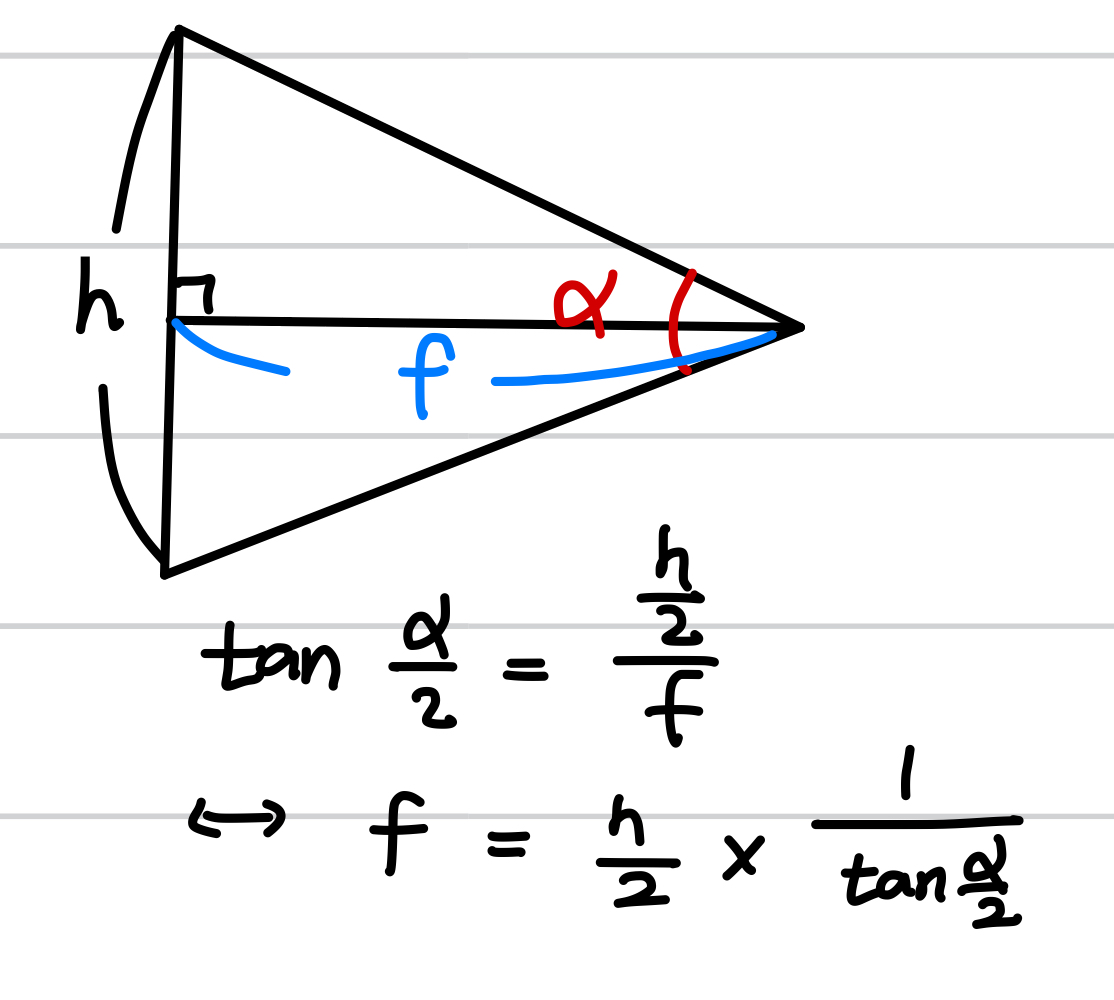
이는 다음과 같은 코드로 나타냅니다 (H == W 일때)

여기까지는 $(u, v, 1)_*^T$ 를 구하는 부분입니다.
이를 생각해보면 z 축의 길이기 1이면서 이미지에서 실제방향으로의 방향벡터입니다.
여기에 이제 extrinsic parameter [R|t] 를 적용합니다.
t는 카메라의 평행이동으로 ray에서의 o가 되고, ($o=t$)
d는 rotation matrix R과 $(u, v, 1)_*^T$ 를 곱한 벡터입니다. ($d = R @ (u, v, 1)_*^T$ : 회전을 적용한 벡터)
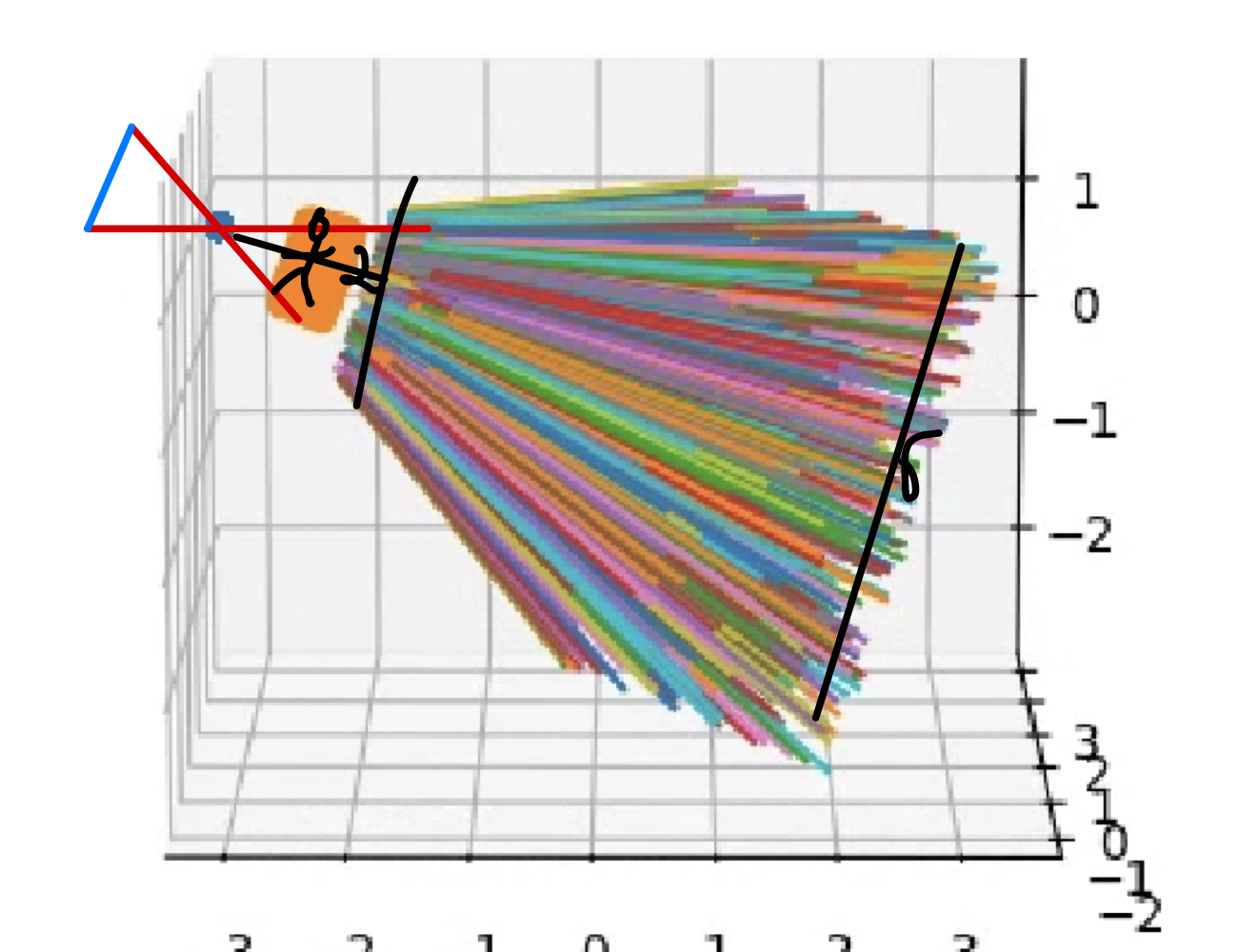
이렇게 r(t) = o + td 를 구하여, (2<= t <=6) 에 대하여 ray를 시각화 해 보면 다음과 같습니다.
하나의 이미지에 대하여 하나의 카메라가 사용되고, 각 픽셀에 할당되는 ray가 다음과 같이 모두 존재합니다.
주황색 부분은 카메라 초점부터 길이가 1인 $(u, v, 1)_*^T$ plane이고,
그 뒤의 직선들은 각 pixel에 대한 ray를 뜻합니다.
4. Volume Rendering
(continuous version)
한 ray를 통한 기대색(expected color) C(r)은 다음과 같습니다.
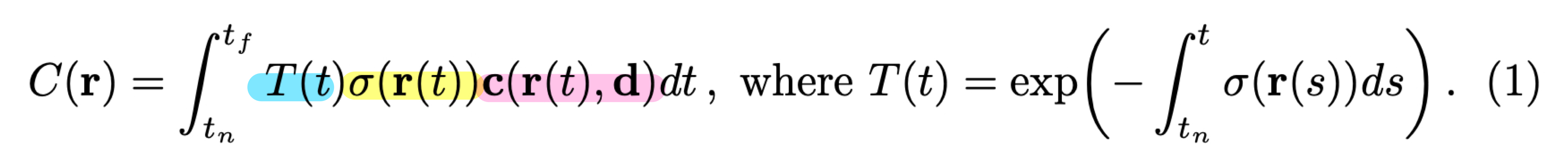
각 파란색, 노란색, 빨간색으로 표현된 요소들은 다음과 같습니다.
$T()$ : transmittance (투과도)
$\sigma()$ : volume density (밀도)
$c()$ : color (색)
$\mathbf{T(t})$ 에 대하여 알아보면, 위 식의 우측에 표현 되어있는데
$y' + \sigma(x) y = 0$ 과 같은 식을 풀어보면, 나오는 제차 1차 미분방정식의 해와 같습니다.
이는 어떤 빛의강도 y의 매우 짧은시간 x에 대한 변화율은 빛의 강도(y)에 특정 함수 $\sigma(x)$를 곱한것과
같다는 의미입니다. 결국 빛의 투과도를 의미하며, 값이 클 수록 투명하고 작을수록 불투명함을 의미합니다.
만약 함수 $\sigma$ 가 constant 라면, $\exp(-\int_{t_n}^{t} \sigma(s) \, ds) = \exp(-\sigma * [t - t_n])$ 입니다.
$\mathbf{\sigma(r(t))}$ 는 빛의 경로위의 있는 물체의 밀도를 나타내는 함수입니다.
NeRF에서는 이 $\sigma$ 함수를 딥뉴럴 네트워크로 학습하게 합니다.
$\mathbf{c(r(t), d)}$ 는 빛의 경로위의 있는 물체의 색을 나타내는 함수입니다.
이 $c$ 함수도 딥뉴럴 네트워크로 학습합니다.
정리하면, 한 픽셀의 색은 (투과도) x (밀도) x (색) 을 한 ray의 모든 지점에(dt) 대하여 적분한 값과 같습니다.
(discrete version)
위의 continuous하게 정의된 수식들을 실제 적분의 구현을 위해 discrete 하게 변경하여 NeRF에 적용합니다.
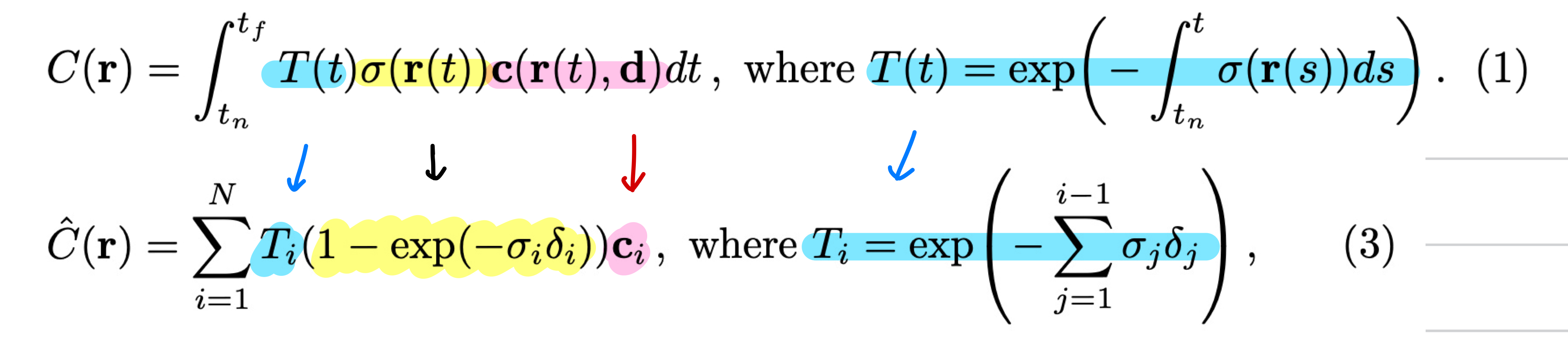
이를 위해 맨 먼저 continuous 한 ray를 discrete 한 점들로 sampling 하는 방법이 필요합니다.
논문에서는 어떤 구간(bin) 안에서 sampling 하는 방식을 사용합니다.
구현에서는 coarse 모델에서 N이 64로 지정합니다.
즉 하나의 ray에 64개의 구간을 나눠놓고 그 안에서 uniform 하게 sampling 하는 방식으로 ray 위의 점들을 뽑습니다.
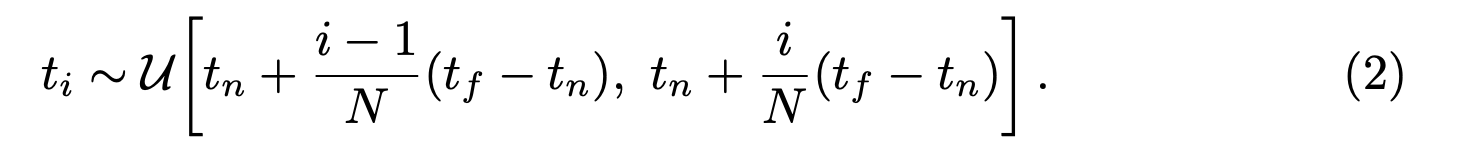
ti 들을 시각화하면 다음 그림처럼 ray들이 점들로 sampling 된 것을 볼 수 있습니다.
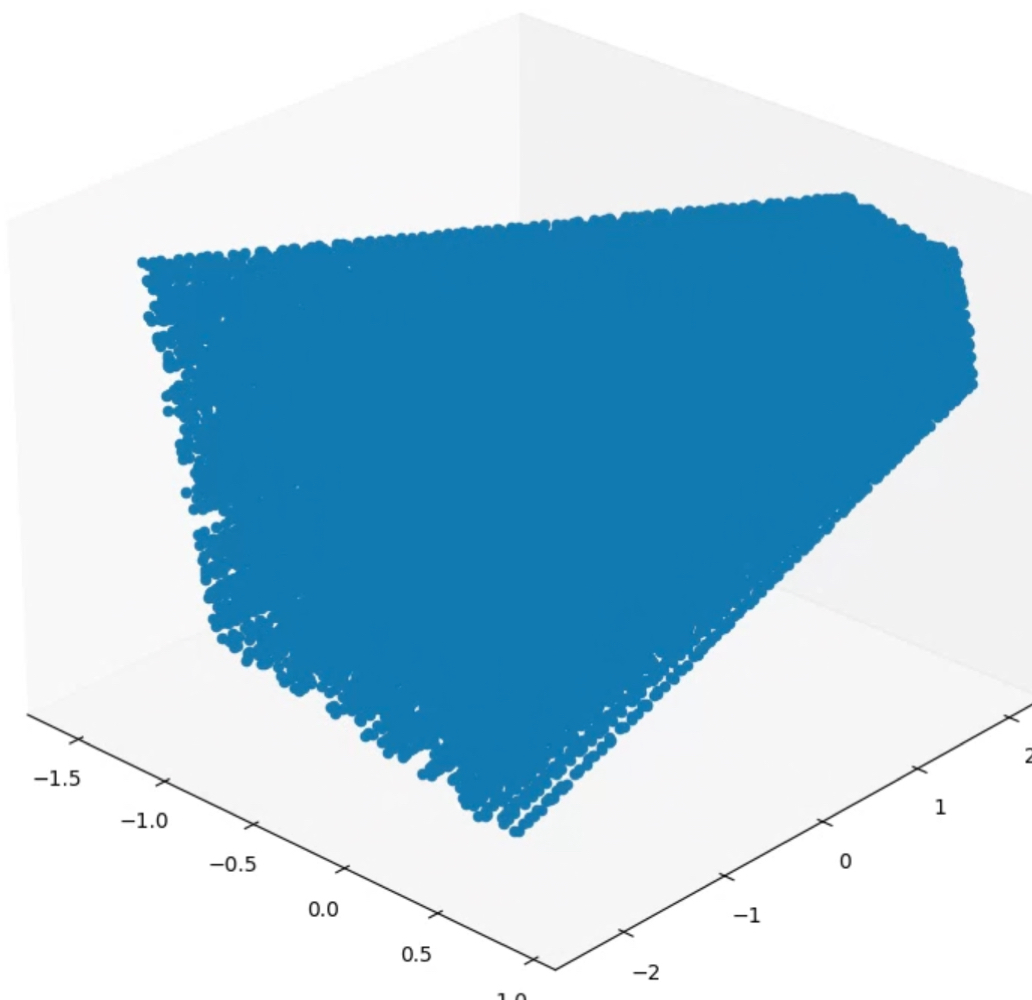
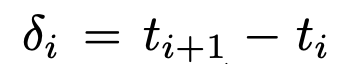
수식(3)에서 사용하는 delta 는 위와 같고, Ti 는 적분대신 합으로, ci 는 네트워크의 output으로 만들어집니다.
그런데 density를 뜻하는 $\sigma$ 는 $1-exp(-\sigma_i \delta_i)$ 로 변경이 됩니다.
논문에서도 별다른 설명이 없고 전통적으로 알파 합성을 사용한다고 합니다.
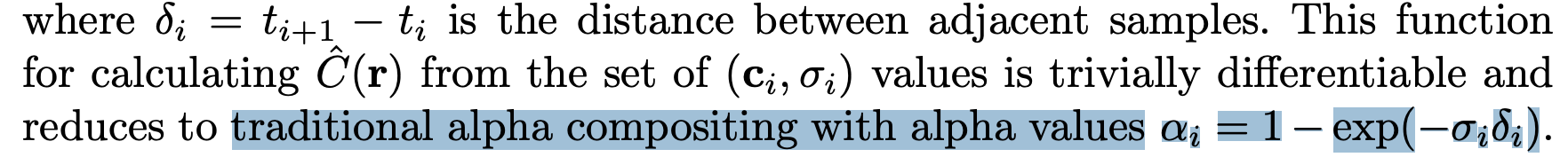
수식(1)의 density처럼 원래는 수식 (3)의 노란 부분이 $\sigma_i \delta_i$ 가 되야 할것 같습니다.
그러나 $\alpha = 1-exp(-\sigma_i \delta_i)$ 인데, 이를 Talyer Extension 으로 확장을 해 보면 다음과 같습니다.
결국 $\sigma_i \delta_i$ 는 테일러 급수의 큰 두항을 사용해 근사를 한 것으로 볼 수 있습니다.
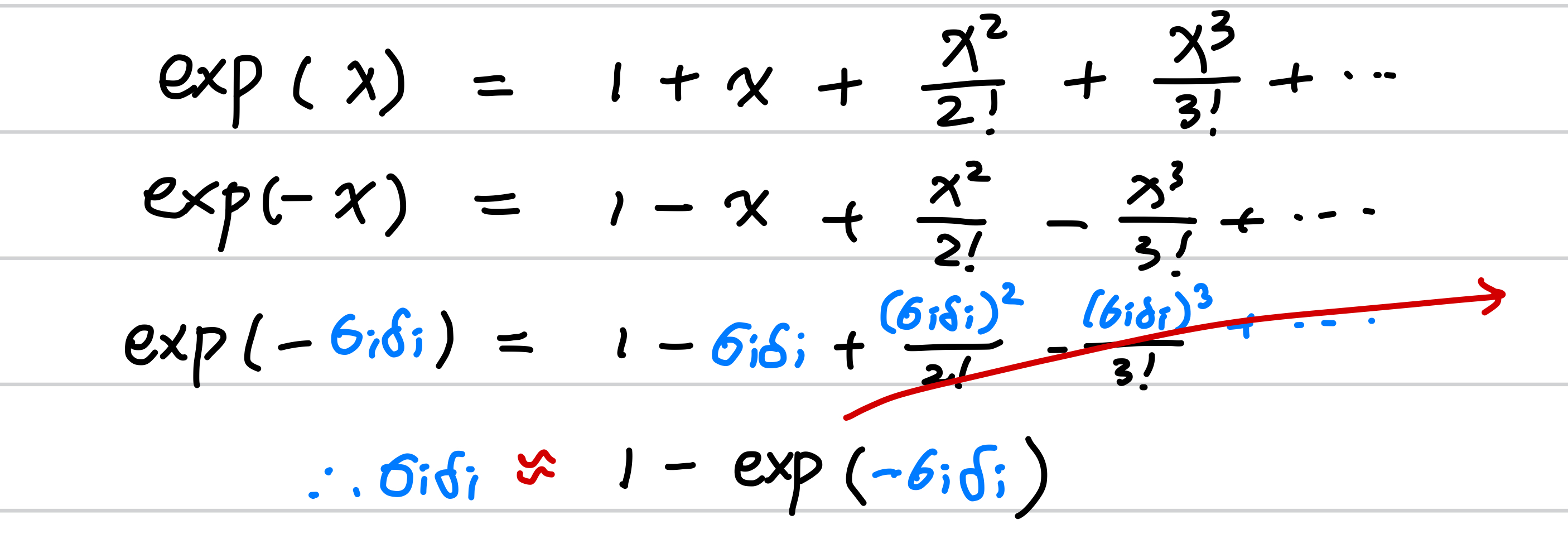
반갑게도 이 사실을 다음 레퍼런스에서 찾을 수 있었습니다.
https://www3.cs.stonybrook.edu/~mueller/papers/volvisOverview.pdf

논문에서 [26]의 레퍼런스를 보면, opacity(불투명도)는 다음과 같이 사용되고,
이는 discrete 한 volume rendering의 density로 쓰이는 것을 알 수 있습니다.
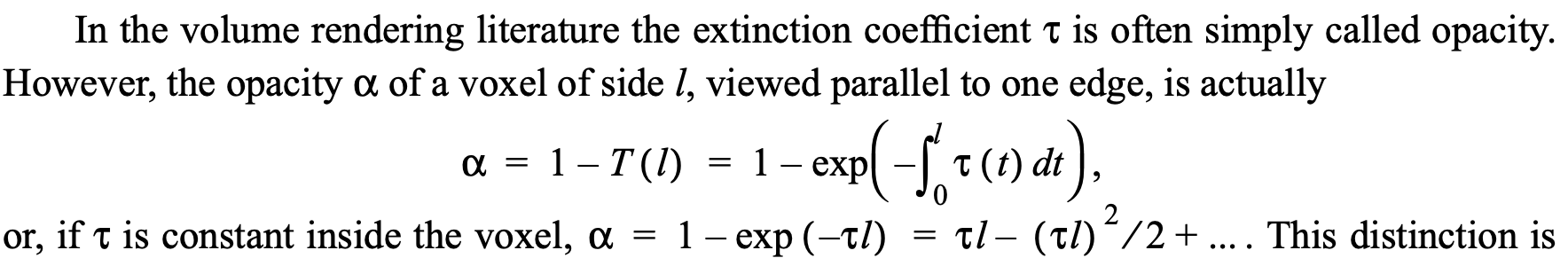
즉 수식(1)의 밀도라는 함수를 수식(3)처럼 불투명도함수를 이용한 것으로 보입니다.
의미적으로 불투명한 정도가 물체의 밀도를 나타낼 수 있기 때문에 opacity를 사용한 것으로 보입니다.
정리하자면 수식(3)은 다음과 같이 확장됩니다. 아래 수식이 실제 구현에 사용됩니다.
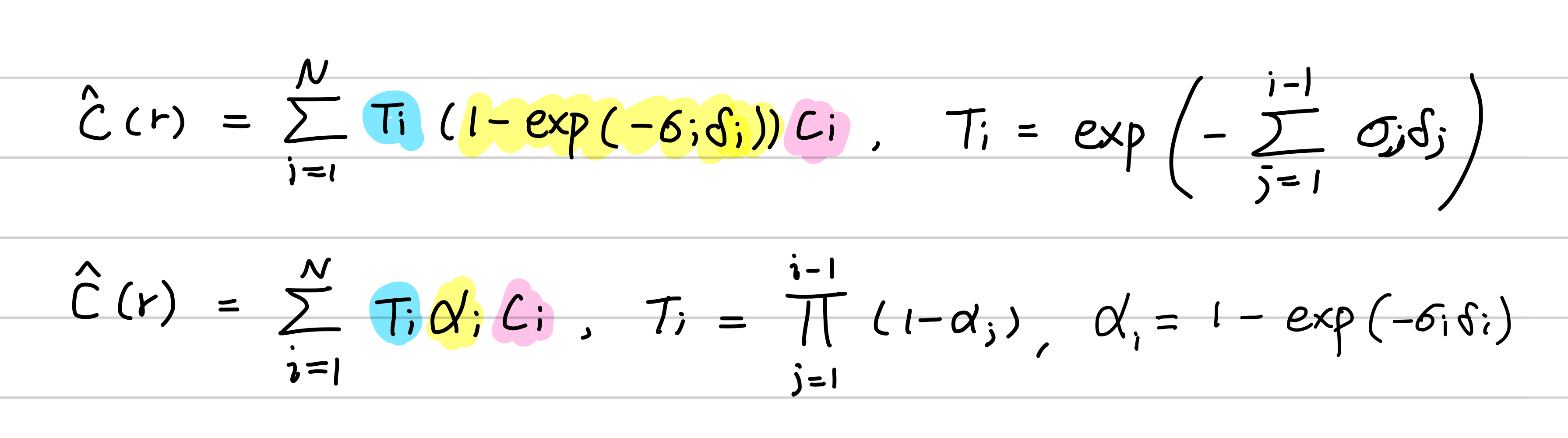
5. Neural Network in NeRF
이제 드디어 NeRF에서의 neural network에 대하여 설명해 보겠습니다.
여태까지 설명한 부분은 Ray 와 같이 input 데이터를 만드는 부분 (pre-processing)
네트워크 아웃풋($\sigma_i, c_i$)으로 색을 만드는 부분 (post-processing) 을 설명하였습니다.
이번 챕터에서는 PE, Model, Loss 그리고
인풋과 아웃풋의 프로세스로 간단히 NeRF의 진행과정을 설명해보려 합니다.
5.1 positional encoding
레퍼런스 [35]에서는 neural network 는 low frequency function 을 학습하는데 bias 되어있다고 합니다.
그리고 뉴럴 네트워크의 입력전에 고주파 함수를 사용하여 더 높은 공간에 매핑한 입력을 사용하면, 고주파 변동이
포함된 데이터를 더 잘 학습한다고 합니다.
이말인즉슨, 네트워크의 입력을 단순히 (x, y, z, phi, theta) 로 하는 것 보다
그보다 높은 차원으로 매핑하는 특정 function을 이용하면 고주파의 색, 기하를 더 잘 표현할 수
있다고 하고 성능도 높아지는 것을 보입니다.
NeRF에서는 다음과 같은 함수를 이용합니다.
$\gamma (.) : \mathbb{R} \rightarrow \mathbb{R}^{2L}$
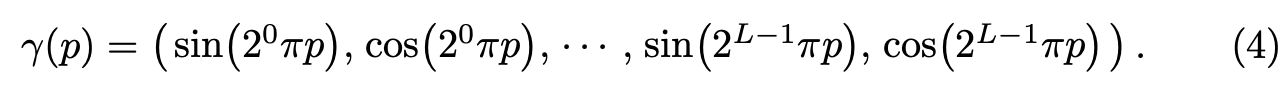
여기서 계산되는 p는 sampling된 점들의 3차원 위치 혹은 3차원 view direction 입니다.
위의 gif 들은 논문에서 나온것과 같은 positional encoding을 사용한 결과이고,
아래 gif 들은 PE 를 적용하지 않은 결과입니다. 확실히 detail 들이 떨어지는 모습을 볼 수 있습니다.




5.2 model
이제 모델에 대하여 알아보겠습니다.
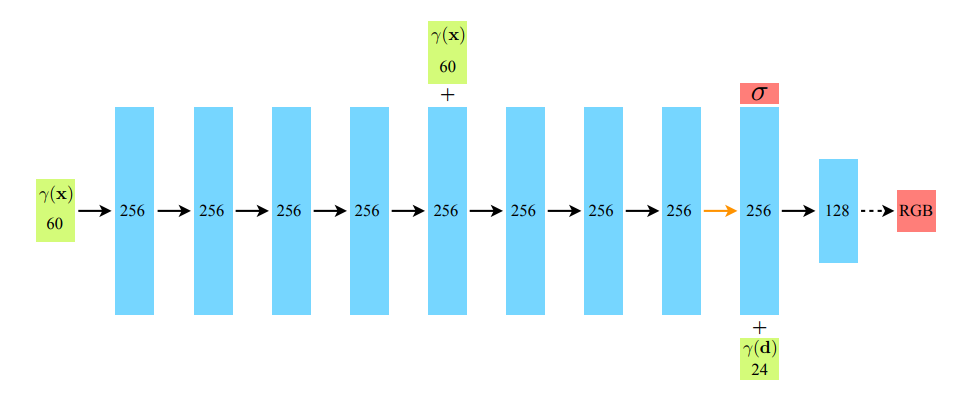
검은색 화살표는 linear + activation fn(ReLU), 이고
노란색 화살표는 activation 이 없는 layer 입니다.
dash 화살표는 sigmoid activation 을 이용한 layer 입니다.
+ 는 concatenation 을 뜻합니다.
output은 sigma/RGB 이고,
예시 코드는 다음과 같습니다.
class NeRF(nn.Module):
def __init__(self, width: int, input_ch: int, input_ch_d: int):
super(NeRF, self).__init__()
self.input_ch_x = input_ch
self.input_ch_d = input_ch_d
# 4 layers
self.linear_x1 = nn.Sequential(nn.Linear(input_ch, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True))
# 4 layers
self.linear_x2 = nn.Sequential(nn.Linear(width + input_ch, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True),
nn.Linear(width, width),
nn.ReLU(inplace=True))
# density
self.linear_density = nn.Linear(width, 1)
# color
self.linear_x3 = nn.Linear(width, width)
self.linear_color = nn.Sequential(nn.Linear(input_ch_d + width, width//2),
nn.ReLU(inplace=True),
nn.Linear(width // 2, 3)
)
def forward(self, x):
input_x, input_d = torch.split(x, [self.input_ch_x, self.input_ch_d], dim=-1)
x = self.linear_x1(input_x)
x = torch.cat([input_x, x], dim=-1)
x = self.linear_x2(x)
# density
out1 = self.linear_density(x)
# color
x = self.linear_x3(x)
x = torch.cat([x, input_d], dim=-1)
out2 = self.linear_color(x)
result = torch.cat([out1, out2], dim=-1)
return result
5.3 learning process
학습 과정은 다음과 같습니다.
먼저 이미지에서 ray 의 갯수를 sampling 합니다. (1024, 4096...)
예를들어 400 x 400 의 input중 1024 개의 pixel을 고릅니다.
이후 그림 7과 같이 각 ray에서 64개의 점들을 sampling 합니다.
[1024 * 64, 3] 의 인풋은 positional embedding 을 통해 [1024 * 64 * 63 / 27] 로 변하고
이를 네트워크의 인풋으로 넣으면, density $\sigma$ [1024 * 64, 1] 그리고 color c = [1024 * 64, 3]
의 ouput을 출력하고 이를 수식(3) 을 통해 volume rendering 을 수행하고
각 ray의 색을 정하게 됩니다.
5.4 loss
정답 픽셀의 색과 네트워크 아웃풋을 통해 볼륨 렌더링된 색을
L2 norm 을 이용하여 loss를 구성합니다.
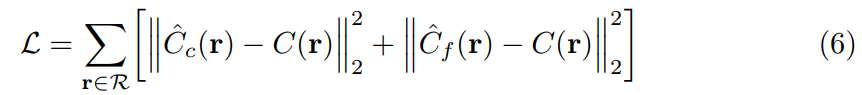
5.5 Hierarchical volume sampling
NeRF는 2개의 모델로 학습이 이뤄집니다.
첫번째는 "coarse" model 로 ray에서 수식(2)의 stratifeid sampling 을 이용하여 point 를 sampling 합니다.
첫번째 모델의 output에서 다음과 같이 $w_i = T_i \times \alpha_i$ 로 정하고
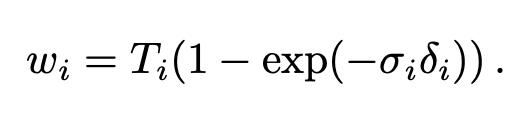
coarse model의 normalized 한 w의 확률분포에 대한 pdf 를 $\hat{w_i} = w_i / \sum_j^{N_c} w_j$ 라고 할 때,
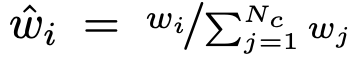
이 분포를 따르는 두번째 네트워크 "fine"의 point들을 sampling 합니다.
이때 Inverse CDF Method를 이용합니다. (논문에서는 Inverse transform sampling 이라고 언급됨)
1. PDF 를 구한다.
2. PDF를 이용해서 CDF 구한다. (누적합)
3. CDF의 y값을 (0~1)에서 unifrom sampling 하여 그 y에 해당하는 x를 구한다.
4. 이때 x는 PDF를 따르는 새로운 sampling을 구할수 있다.
https://m.blog.naver.com/jinis_stat/221648391742
Sampling 방법 / Inverse CDF Method
Sampling Methods 앞으로 monte carlo 섹션에서의 포스팅에서는, 샘플링 방법(Sampling Method)에 대해...
blog.naver.com
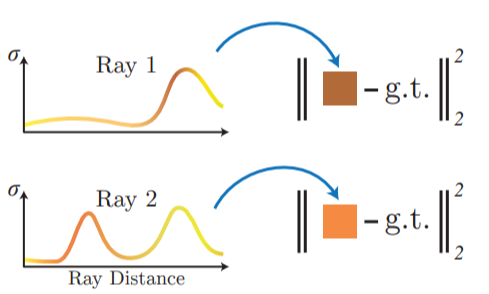
다음 그림과 같이 Ray1 에서 뽑은 sample points(64개)의 PDF 를 따르는
더 빽빽한 ("fine"한) Ray2의 sample points(128개) 들을 뽑을 수 있고 마지막 결과는
"coarse" 와 "fine"에서 뽑은 모든 sample 들 (192개) 를 이용한다.
6. Results
이제 결과를 볼 차례입니다.
데이터셋은 synthetic data, llff data, deep voxel data를 이용하였습니다.
당시 비교한 알고리즘과 큰 차이를 보이며 좋은 성능을 보였습니다.
6.1 ablation study

논문은 다양한 ablation study를 통해서 어떤 요소가 성능에 도움이 되는지 분석하였습니다.
(1) Positional Encoding 이 없고, view direction 도 없고 Hierchical architecture 도 없다.
(2) ~ (4) 는 각 요소를 하나씩 바꾸며 줄였는데 Hierarchical 의 도움이 가장 적은것 처럼 보입니다.
(5), (6) 은 학습 이미지의 갯수를 적게 하며
(7), (8) 은 PE의 frequencies의 갯수에 따른 성능평가입니다.
너무 적거나 너무 많아도 성능이 떨어지며 10 이 가장 좋다고 주장합니다.
6.2 qualitative results


NeRF는 모든 데이터셋에서 매우 디테일한 결과를 보여줍니다.
매우 놀라운 결과입니다.
6.3 quantitative results
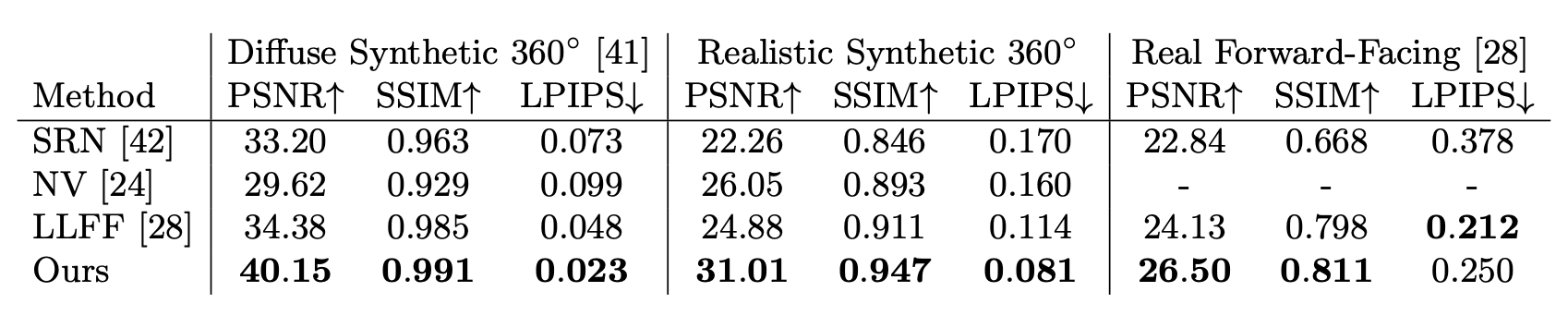
모든 데이터셋에 좋은 결과를 보여주었습니다.
성능 평가는 PSNR, SSIM, LPIPS 를 비교합니다.
7. implementation
필자가 구현한 실제 코드를 참조하시면 이해에 도움이 될 수 있을 것 같습니다. 😎😎
↓ 구현 코드 ↓
https://github.com/csm-kr/nerf_pytorch
GitHub - csm-kr/nerf_pytorch: re-implementation of nerf (Neural Radiance Fields) (ECCV2020)
:blossom: re-implementation of nerf (Neural Radiance Fields) (ECCV2020) - GitHub - csm-kr/nerf_pytorch: re-implementation of nerf (Neural Radiance Fields) (ECCV2020)
github.com
네 이번에는 NeRF에 대하여 알아보았습니다.
질문과 토론은 언제든지 환영합니다. 🤩🤩🤩🤩🤩
감사합니다.
'Nerf' 카테고리의 다른 글
| docker 로 nerfstudio 이용해보기 (0) | 2023.11.14 |
|---|

댓글